
【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,左,右焦点分别为F1,F2,上顶点和右顶点分别为B,A,线段AB的中点为D,且![]() ,△AOB的面积为
,△AOB的面积为![]() .
.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于M,N两点,若△MF2N的面积为![]() ,求以F2为圆心且与直线l相切的圆的方程.
,求以F2为圆心且与直线l相切的圆的方程.
【答案】(1)![]() ;(2)(x-2)2+y2=8.
;(2)(x-2)2+y2=8.
【解析】试题分析:(1)求椭圆方程关键是求方程![]() 中的
中的![]() ,题中有两个已知条件,由
,题中有两个已知条件,由![]() 用数学式子翻译出来联立方程组可解得;(2)先考虑当直线
用数学式子翻译出来联立方程组可解得;(2)先考虑当直线![]() 垂直于
垂直于![]() 轴时是否满足题意,如满足,求出相应圆方程,如不满足,则舍去,当直线
轴时是否满足题意,如满足,求出相应圆方程,如不满足,则舍去,当直线![]() 斜率存在时,可设方程为
斜率存在时,可设方程为![]() ,代入椭圆方程,由椭圆中的弦长公式求出弦长
,代入椭圆方程,由椭圆中的弦长公式求出弦长![]() ,再由点到直线距离公式求出
,再由点到直线距离公式求出![]() 到直线
到直线![]() 的距离,利用已知三角形面积求得
的距离,利用已知三角形面积求得![]() ,从而可得所求圆方程.
,从而可得所求圆方程.
试题解析:(1)设椭圆方程为![]() (a>b>0).由已知得A(a,0),B(0,b),D
(a>b>0).由已知得A(a,0),B(0,b),D![]() ,
,
所以kOD·kAB= ,
,
即a2=2b2,①
又S△AOB=![]() ,所以
,所以![]() ,②
,②
由①②解得a2=8,b2=4,
所以椭圆方程为![]() .
.
(2)①当直线l⊥x轴时,易得M(-2, ![]() ),N(-2,
),N(-2, ![]() ),△MF2N的面积为
),△MF2N的面积为![]() ,不合题意.
,不合题意.
②当直线l与x轴不垂直时,设直线l的方程为y=k(x+2),代入椭圆方程得
(1+2k2)x2+8k2x+8k2-8=0.
显然有Δ>0,设M(x1,y1),N(x2,y2),
则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
所以MN=![]()
= ,
,
化简得MN=![]() .
.
又圆的半径![]() ,
,
所以![]() MN·r
MN·r
=![]() ×
×![]() ·
·![]()
=![]() ,
,
化简得k4+k2-2=0,解得k=±1,
所以r=![]() ,
,
所以所求圆的方程为(x-2)2+y2=8.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ-2cos θ-6sin θ+![]() =0,直线l的参数方程为
=0,直线l的参数方程为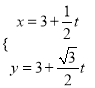 (t为参数).
(t为参数).
(1)求曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,点P的坐标为(3,3),求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,且满足Sn=2n+1+2p(n∈N*).
(1)求p的值及数列{an}的通项公式;
(2)若数列{bn}满足![]() =(3+p)anbn,求数列{bn}的前n项和Tn.
=(3+p)anbn,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人为研究中学生的性别与每周课外阅读量这两个变量的关系,随机抽查了100名中学生,得到频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].

(Ⅰ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生周课外阅读时间的平均数.
(Ⅱ)在样本数据中,有20位女生的每周课外阅读时间超过4小时,15位男生的每周课外阅读时间没有超过4小时.请画出每周课外阅读时间与性别列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“该校学生的每周课外阅读时间与性别有关”.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附: 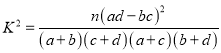
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·无锡模拟)已知函数f(x)满足![]() ,当x∈[0,1]时,f(x)=x.若g(x)=f(x)-mx-2m在区间(-1,1]上有两个零点,则实数m的取值范围是________________.
,当x∈[0,1]时,f(x)=x.若g(x)=f(x)-mx-2m在区间(-1,1]上有两个零点,则实数m的取值范围是________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
A. ①② B. ②③
C. ①③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·日照一模)如图所示,ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,给出下列结论:

①A、M、O三点共线;②A、M、O、A1不共面;③A、M、C、O共面;④B、B1、O、M共面.
其中正确结论的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,如果x∈D,y∈D,使得f(x)=-f(y)成立,则称函数f(x)为“Ω函数”.给出下列四个函数:①y=sin x;②y=2x;③y=![]() ;④f(x)=ln x.则其中“Ω函数”共有( )
;④f(x)=ln x.则其中“Ω函数”共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有两个公共点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com