
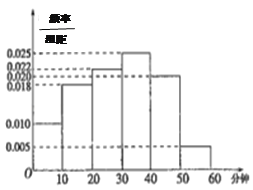
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的2×2列联表,若按95%的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)现在从该地区非体育迷的电视观众中,采用分层抽样方法选取5名观众,求从这5名观众选取两人进行访谈,被抽取的2名观众中至少有一名女生的概率.
附:![]()
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
【答案】(1) 没有95%的可靠性理由认为“体育迷”与性别有关(2) ![]()
【解析】试题分析:(1)根据频数等于总数乘以对应概率,得体育迷总数,再根据关系依次填写列联表,代入公式求得卡方值,对照参考数据作出判断(2)先根据分层抽样得抽取的男女生数,再利用枚举法确定总事件数,从中确定至少有一名女生事件数,最后根据古典概型概率公式求概率
试题解析:解 (1)由频率分布直方图可以知道,在抽取的100人中,
“体育迷”有25人,从而填写列联表如下:
非体育迷 | 体育迷 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
将列联表中的数据代入公式计算,
得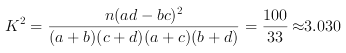 , 因为
, 因为![]() ,
,
所以没有![]() 的可靠性理由认为“体育迷”与性别有关;
的可靠性理由认为“体育迷”与性别有关;
(2)根据分层抽样原理,抽取的男生有![]() 人,记为A,B;
人,记为A,B;
女生有![]() 人,分别记为c、d、e;
人,分别记为c、d、e;
从5人中任取2人,基本事件是AB、Ac、Ad、Ae、Bc、Bd、Be、cd、ce、de共10种,
至少有一名女生的事件是Ac、Ad、Ae、Bc、Bd、Be、cd、ce、de共9种,
故所求的概率为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为 ![]() 阶“期待数列”:
阶“期待数列”:
① ![]() ;
;
② ![]() .
.
(1)分别写出一个单调递增的 3 阶和 4 阶“期待数列”.
(2)若某 2017 阶“期待数列”是等差数列,求该数列的通项公式.
(3)记 ![]() 阶“期待数列”的前
阶“期待数列”的前 ![]() 项和为
项和为 ![]() ,试证:
,试证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在甲、乙两个电视台做总时间不超过 300 分钟的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.设该公司在甲、乙两个电视台做广告的时间分别为![]() 分钟和
分钟和![]() 分钟.
分钟.
(Ⅰ)用![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(Ⅱ)该公司如何分配在甲、乙两个电视台做广告的时间使公司的收益最大,并求出最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与抛物线
与抛物线![]() 相交于不同两点
相交于不同两点![]() 、
、![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求抛物线![]() 的焦点到准线的距离;
的焦点到准线的距离;
(2)若直线![]() 又与圆
又与圆![]() 相切于点
相切于点![]() ,且
,且![]() 为线段
为线段![]() 的中点,求直线
的中点,求直线![]() 的方程;
的方程;
(3)若![]() ,点
,点![]() 在线段
在线段![]() 上,满足
上,满足![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点M(﹣2,﹣1),离心率为
经过点M(﹣2,﹣1),离心率为![]() .过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
(Ⅰ)求椭圆C的方程;
(Ⅱ)试判断直线PQ的斜率是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,通项
,通项![]() 满足
满足![]() (
(![]() 是常数,
是常数, ![]() 且
且![]() ).
).
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)当![]() 时,证明
时,证明![]() ;
;
(Ⅲ)设函数![]() ,
, ![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 对
对![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(某保险公司有一款保险产品的历史户获益率(获益率=获益÷保费收入)的频率分布直方图如图所示:
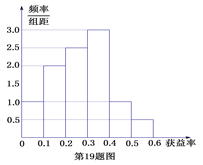
(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验若每份保单的保费在![]() 元的基础上每增加
元的基础上每增加![]() 元,对应的销量
元,对应的销量![]() (万份)与
(万份)与![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下
(元)有较强线性相关关系,从历史销售记录中抽样得到如下![]() 组
组![]() 与
与![]() 的对应数据:
的对应数据:
|
|
|
|
|
|
销量 |
|
|
|
|
|
(ⅰ)根据数据计算出销量![]() (万份)与
(万份)与![]() (元)的回归方程为
(元)的回归方程为![]() ;
;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
参考公示: 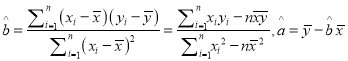
查看答案和解析>>
科目:高中数学 来源: 题型:
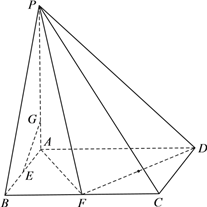
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA![]() 面ABCD,且AB=2,AD=4,
面ABCD,且AB=2,AD=4,
AP=4,F是线段BC的中点.
⑴ 求证:面PAF![]() 面PDF;
面PDF;
⑵ 若E是线段AB的中点,在线段AP上是否存在一点G,使得EG![]() 面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com