
【题目】在直角坐标系![]() 中,曲线C的方程为
中,曲线C的方程为![]() ,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求直线l的直角坐标方程;
(2)已知P是曲线C上的一动点,过点P作直线![]() 交直线于点A,且直线
交直线于点A,且直线![]() 与直线l的夹角为45°,若
与直线l的夹角为45°,若![]() 的最大值为6,求a的值.
的最大值为6,求a的值.
科目:高中数学 来源: 题型:
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.他们的调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | |||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,如图,
,如图,![]() 分别交
分别交![]() 轴正半轴于点
轴正半轴于点![]() .射线
.射线![]() 分别交
分别交![]() 于点
于点![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 轴垂直,直线
轴垂直,直线![]() 与
与![]() 轴垂直.
轴垂直.

(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交曲线
交曲线![]() 与点
与点![]() ,射线
,射线![]() 与点
与点![]() ,且交曲线
,且交曲线![]() 于点
于点![]() .问:
.问:![]() 的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场更新技术培育了一批新型的“盆栽果树”,这种“盆栽果树”将一改陆地栽植果树只在秋季结果的特性,能够一年四季都有花、四季都结果.现为了了解果树的结果情况,从该批果树中随机抽取了容量为120的样本,测量这些果树的高度(单位:厘米),经统计将所有数据分组后得到如图所示的频率分布直方图.
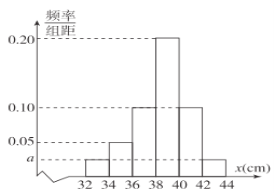
(1)求![]() ;
;
(2)已知所抽取的样本来自![]() 两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
(i)请将图中列联表补充完整,并判断是否有![]() 的把握认为“优品盆栽”与
的把握认为“优品盆栽”与![]() 两个实验基地有关?
两个实验基地有关?
优品 | 非优品 | 合计 | |
| 60 | ||
| 20 | ||
合计 |
(ii)用样本数据来估计这批果树的生长情况,若从该农场培育的这批“盆栽果树”中随机抽取4棵,求其中“优品盆栽”的棵树![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校近几年来通过“书香校园”主题系列活动,倡导学生整本阅读纸质课外书籍.下面的统计图是该校2013年至2018年纸质书人均阅读量的情况,根据统计图提供的信息,下列推断不合理的是( )
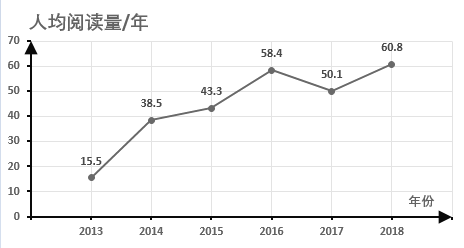
A.从2013年到2016年,该校纸质书人均阅读量逐年增长
B.2013年至2018年,该校纸质书人均阅读量的中位数是46.7本
C.2013年至2018年,该校纸质书人均阅读量的极差是45.3本
D.2013年至2018年,该校后三年纸质书人均阅读量总和是前三年纸质书人均阅读量总和的2倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=![]() 有如下四个命题:
有如下四个命题:
①f(x)的图像关于y轴对称.
②f(x)的图像关于原点对称.
③f(x)的图像关于直线x=![]() 对称.
对称.
④f(x)的最小值为2.
其中所有真命题的序号是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com