
【题目】正方体![]() 的棱长为2,
的棱长为2,![]() 分别为
分别为![]() 的中点,则( )
的中点,则( )
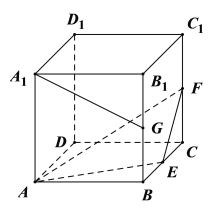
A.直线![]() 与直线
与直线![]() 垂直B.直线
垂直B.直线![]() 与平面
与平面![]() 平行
平行
C.平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() D.点
D.点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等
的距离相等
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 过定点A(1,0).
过定点A(1,0).
(Ⅰ)若![]() 与圆相切,求
与圆相切,求![]() 的方程;
的方程;
(Ⅱ)若![]() 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又![]() 与
与![]() 的交点为N,求证:
的交点为N,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC![]() AB=2,且平面PAD⊥平面ABCD.
AB=2,且平面PAD⊥平面ABCD.
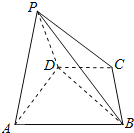
(1)证明:BD⊥平面PAD
(2)求点C到平面PBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ADEF与梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
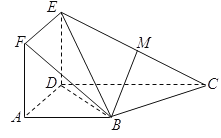
(1)求证:BM∥平面ADEF;
(2)求证:平面BDE⊥平面BEC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知BD为圆锥AO底面的直径,若![]() ,C是圆锥底面所在平面内一点,
,C是圆锥底面所在平面内一点,![]() ,且AC与圆锥底面所成角的正弦值为
,且AC与圆锥底面所成角的正弦值为![]() .
.
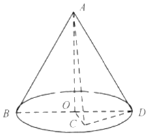
(1)求证:平面![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|,关于x的不等式f(x)<3﹣|2x+1|的解集记为A.
(1)求A;
(2)已知a,b∈A,求证:f(ab)>f(a)﹣f(b).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
有时可用函数

描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(![]() ),
),![]() 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1) 证明:当![]() 时,掌握程度的增加量
时,掌握程度的增加量![]() 总是下降;
总是下降;
(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为![]() ,
,![]() ,
,
![]() .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com