练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
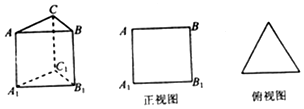
    5．如图所示，水平放置的三棱柱的侧棱长和底面边长均为1，且侧棱A A1⊥面A1 B1C1，正视图是边长为1的正方形，该三棱柱的侧视图面积为（　　）
    A．3B．$2\sqrt{3}$C．$\frac{{\sqrt{3}}}{2}$D．$\sqrt{3}$

    分析 由三视图和题意可知三棱柱是正三棱柱，结合正视图，俯视图，不难得到侧视图，然后求出面积．

    解答 解：由三视图和题意可知三棱柱是正三棱柱，底面边长为1，侧棱长1，
    结合正视图，俯视图，得到侧视图是矩形，长为1，宽为$\frac{\sqrt{3}}{2}$
    面积为：$\frac{\sqrt{3}}{2}$．
    故选C．

    点评 本题考查由三视图求侧视图的面积，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．如图是由选项图中哪个平面图形旋转得到的（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若函数$y=\sqrt{k{x^2}+kx+3}$的定义域为R，则k的取值范围是（　　）
    A．（-∞，0]∪[12，+∞）B．（-∞，0）∪（12，+∞）C．（0，12）D．[0，12]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．扇形的圆心角为$θ=\frac{3}{2}$弧度，半径为4cm，则扇形的面积是12cm2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知直线m、n与平面α、β，则下列说法正确的是（　　）
    A．若m∥α，n∥α，则m∥nB．若m∥α，n⊥α，则n⊥mC．若m⊥α，n⊥β，则α⊥βD．若m⊥α，n⊥β，则n⊥m

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．在小时候，我们就用手指练习过数数．一个小朋友按如图所示的规则练习数数，数到2015时对应的指头是中指．（填出指头的名称，各指头的名称依次为大拇指、食指、中指、无名指、小指）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知等式：
    cos261°+sin231°+cos61°sin31°=a
    cos266°+sin236°+cos66°sin36°=a
    cos220°+sin210°+cos20°sin（-10°）=a
    cos28°+sin222°+cos8°sin（-22°）=a
    （Ι）根据以上所给的等式归纳出一个具有一般性的等式，并指出实数a的值
    （Ⅱ）证明你写的等式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若圆x2+y2-ax-2=0与抛物线y2=4x的准线相切，则a的值是1 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知抛物线C：y2=4x的焦点为F，直线y=x-2与C交于A，B两点，
    （I）求线段AB的长；
    （II）求三角形ABF的周长．

    查看答案和解析>>

    同步练习册答案