练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，△ABC中，AB＝8，BC＝10，AC＝6，DB⊥平面ABC，且AE∥FC∥BD，BD＝3，FC＝4，AE＝5，求此几何体的体积．

    【答案】96

    【解析】试题分析：，取CM＝AN＝BD，连接DM，MN，DN，用“分割法”把原几何体分割成一个直三棱柱和一个四棱锥．所以V几何体＝V三棱柱＋V四棱锥．

    试题解析：

    如图，取CM＝AN＝BD，连接DM，MN，DN，用“分割法”把原几何体分割成一个直三棱柱和一个四棱锥．所以V几何体＝V三棱柱＋V四棱锥．由题知三棱柱ABCNDM的体积为V1＝×8×6×3＝72.

    四棱锥DMNEF的体积为V2＝S梯形MNEF·DN＝××(1＋2)×6×8＝24，

    则几何体的体积为V＝V1＋V2＝72＋24＝96.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，判断函数的奇偶性并证明；

    （2）讨论的零点个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“共享单车”的出现，为我们提供了一种新型的交通方式．某机构为了调查人们对此种交通方式的满意度，从交通拥堵不严重的 城市和交通拥堵严重的 城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图（如图所示）：

    合计

    认可

    不认可

    合计

    （Ⅰ）若得分不低于80分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此 列联表，并据此样本分析是否有 的把握认为城市拥堵与认可共享单车有关；
    （Ⅱ）若从此样本中的 城市和 城市各抽取1人，则在此2人中恰有一人认可的条件下，此人来自 城市的概率是多少？
    附：参考数据：（参考公式： ）

    0.150

    0.100

    0.050

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某志愿者到某山区小学支教，为了解留守儿童的幸福感，该志愿者对某班40名学生进行了一次幸福指数的调查问卷，并用茎叶图表示如下（注：图中幸福指数低于70，说明孩子幸福感弱；幸福指数不低于70，说明孩子幸福感强）.

    （Ⅰ）根据茎叶图中的数据完成 列联表，并判断能否有 的把握认为孩子的幸福感强与是否是留守儿童有关？

    （Ⅱ）从15个留守儿童中按幸福感强弱进行分层抽样，共抽取5人，又在这5人中随机抽取2人进行家访，求这2个学生中恰有一人幸福感强的概率.
    参考公式： ； 附表：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥V-ABC中，平面VAB平面ABC， VAB为等边三角形，ACBC且AC=BC=，O,M分别为AB,VA的中点。

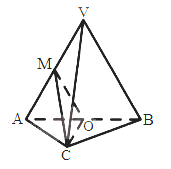
    （I）求证：VB//平面MOC；

    （II）求证：平面MOC平面VAB；

    （III）求三棱锥V-ABC的体积。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（其中，为常量，且，的图象经过点，．

    （）求，的值．

    （）当时，函数的图像恒在函数图像的上方，求实数的取值范围．

    （）定义在上的一个函数，如果存在一个常数，使得式子对一切大于的自然数都成立，则称函数为“上的函数”（其中，．试判断函数是否为“上的函数”．若是，则求出的最小值；若不是，则请说明理由．（注：）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在R上的奇函数f（x）满足f（x﹣2）=f（x+2），且当x∈[﹣2，0]时，f（x）=3x﹣1，则f（9）=（ ）
    A.﹣2
    B.2
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某教育机构随机抽查某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以5为组距将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是(　　)

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）是定义在R上的周期为2的奇函数，当0＜x＜1时，f（x）=2x（1﹣x），则f（﹣ ）+f（1）=（ ）
    A.﹣
    B.﹣
    C.
    D.

    查看答案和解析>>

    同步练习册答案