
求过定点P(2,3)且在两坐标轴上截距相等的直线方程.
|
解法 1:设直线的两截距皆为a,则有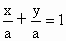 . ① . ①
即 x+y=a,将点P(2,3)代入,得a=5.∴所求的直线方程为x+y=5.这种解法是有问题的,问题在于:所设直线方程 ①不包括两截距都是零的情况.应增补两截距为零的情况.当直线两截距都是零时,设直线方程为 y=kx,将P(2,3)代入得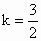 . .
∴ 所求直线方程为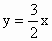 ,即3x-2y=0.综上所述,所求直线方程为x+y-5=0,或3x-2y=0. ,即3x-2y=0.综上所述,所求直线方程为x+y-5=0,或3x-2y=0.
利用截距式解题. 解法 2:由已知直线的斜率存在,设所求直线方程为y-3=k(x-2).令 y=0解得横截距为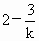 ,令x=0解得纵截距为3-2k. ,令x=0解得纵截距为3-2k.
已知直线在两轴上的截距相等,得 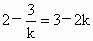 ,解得 ,解得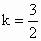 ,或k=-1. ,或k=-1.
故所求直线方程为 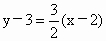 或y-3=-(x-2), 或y-3=-(x-2),
即 3x-2y=0,或x+y-5=0.利用点斜式求解. |


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修2) 2009-2010学年 第20期 总176期 人教课标高一版 题型:044
求过定点P(2,3),且在两坐标轴上的截距互为相反数的直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com