
如图,点![]() 为圆形纸片内不同于圆心
为圆形纸片内不同于圆心![]() 的定点,动点
的定点,动点![]() 在圆周上,将纸片折起,使点
在圆周上,将纸片折起,使点![]() 与点
与点![]() 重合,设折痕
重合,设折痕![]() 交线段
交线段![]() 于点
于点![]() .现将圆形纸片放在平面直角坐标系
.现将圆形纸片放在平面直角坐标系![]() 中,设圆
中,设圆![]() :
:![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
⑴证明曲线![]() 是椭圆,并写出当
是椭圆,并写出当![]() 时该椭圆的标准方程;
时该椭圆的标准方程;
 ⑵设直线
⑵设直线![]() 过点
过点![]() 和椭圆
和椭圆![]() 的上顶点
的上顶点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,若椭圆
,若椭圆![]() 的离心率
的离心率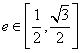 ,求点
,求点![]() 的纵坐标的取值范围.
的纵坐标的取值范围.
解:⑴依题意得,直线m为线段AM的中垂线,∴NA=NM
∴NC+NA=NC+NM=CM=2a>2。
∴N点的轨迹是以C、A为焦点,长轴为2a,焦距为2的椭圆。 ……………4分
当a=2时,2a=4,焦距2C=2 ∴b2=3
∴椭圆方程为![]() 。 ……………………………………………………………6分
。 ……………………………………………………………6分
⑵设椭圆的标准方程为![]() ,由⑴知:b2=a2−1
,由⑴知:b2=a2−1
又C(−1,0),B(0,b),
∴直线l的方程为![]() ,即bx−y+b=0 …………………………8分
,即bx−y+b=0 …………………………8分
设Q(x,y),因为点Q与点A(1,0)关于直线l对称。
∴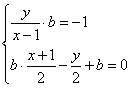 ,消去x,得:
,消去x,得:![]() …………………………10分
…………………………10分
∵离心率e∈[![]() ,
,![]() ], ∴
], ∴![]() ≤e2≤
≤e2≤![]() , 即
, 即![]() ≤
≤![]() ≤
≤![]() , ∴
, ∴![]() ≤a2≤4 ……………12分
≤a2≤4 ……………12分
∴![]() ≤b2+1≤4,即
≤b2+1≤4,即![]() ≤b≤
≤b≤![]() 。
。
∴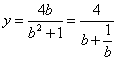 ≤2,当且仅当b=1时取等号。 ……………………14分
≤2,当且仅当b=1时取等号。 ……………………14分
又当b=![]() 时,y=
时,y=![]() ;当b=
;当b=![]() 时,y=
时,y=![]() ,∴
,∴![]() ≤y≤2。
≤y≤2。
∴点Q的纵坐标的取值范围时[![]() ,2]。 ………………………………16分
,2]。 ………………………………16分


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
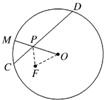 3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( )
3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( )查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.
如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.| 1 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于P,则点P的轨迹是
如图一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于P,则点P的轨迹是查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省扬州市宝应县高三下学期期初测试数学试卷 题型:解答题
(本题满分15分)如图,点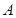 为圆形纸片内不同于圆心
为圆形纸片内不同于圆心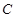 的定点,动点
的定点,动点 在圆周上,将纸片折起,使点
在圆周上,将纸片折起,使点 与点
与点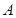 重合,设折痕
重合,设折痕 交线段
交线段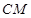 于点
于点 .现将圆形纸片放在平面直角坐标系
.现将圆形纸片放在平面直角坐标系 中,设圆
中,设圆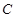 :
: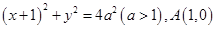 ,记点
,记点 的轨迹为曲线
的轨迹为曲线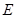 .
.
⑴证明曲线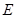 是椭圆,并写出当
是椭圆,并写出当 时该椭圆的标准方程;
时该椭圆的标准方程;
⑵设直线 过点
过点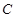 和椭圆
和椭圆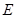 的上顶点
的上顶点 ,点
,点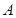 关于直线
关于直线 的对称点为点
的对称点为点 ,若椭圆
,若椭圆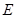 的离心率
的离心率 ,求点
,求点 的纵坐标的取值范围.
的纵坐标的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com