
【题目】某投资公司在2020年年初准备将1000万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利40%,也可能亏损10%,且这两种情况发生的概率分别为![]() 和
和![]() ;
;
项目二:通信设备据市场调研,投资到该项目上,到年底可能获利50%,可能损失30%,也可能不赔不赚,且这三种情况发生的概率分别为![]() ,
,![]() 和
和![]() .针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
.针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
【答案】投资项目一更合理,理由见解析
【解析】
根据题意,写出两个项目的获利的分布列,再根据离散型分布列分别写出期望![]() 和
和![]() ,再求出两个项目的获利的方差
,再求出两个项目的获利的方差![]() 和
和![]() ,比较两个项目的期望和方差,利用期望和方差的意义,即可得出结论.
,比较两个项目的期望和方差,利用期望和方差的意义,即可得出结论.
解:由题意知,项目一:到年底可能获利40%,也可能亏损10%,
且这两种情况发生的概率分别为![]() 和
和![]() ,
,
若按“项目一”投资,设获利![]() 万元,
万元,
![]() 的分布列为:
的分布列为:
| 400 | -100 |
|
|
|
![]()
![]() (万元);
(万元);
而项目二:到年底可能获利50%,可能损失30%,也可能不赔不赚,
且这三种情况发生的概率分别为![]() ,
,![]() 和
和![]() ,
,
若按“项目二”投资,设获利![]() 万元,则
万元,则![]() 的分布列为:
的分布列为:
| 500 | -300 | 0 |
|
|
|
|
![]()
![]() (万元);
(万元);
又![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
这说明虽然项目一、项目二获利相等,但项目一更稳妥,
综上所述,该投资公司投资项目一更合理.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,![]() 是以PF为底边的等腰三角形,PA平行于x轴,点
是以PF为底边的等腰三角形,PA平行于x轴,点![]() ,且点P在直线
,且点P在直线![]() 上运动.记点A的轨迹为C.
上运动.记点A的轨迹为C.
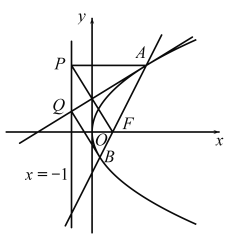
(1)求C的方程.
(2)直线AF与C的另一个交点为B,等腰![]() 底边的中线与直线
底边的中线与直线![]() 的交点为Q,试问
的交点为Q,试问![]() 的面积是否存在最小值?若存在,求出该值;若不存在,请说明理由.
的面积是否存在最小值?若存在,求出该值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个简单图中两两相邻的t个项点称为一个团,与其余每个顶点均相邻的顶点称为中心点.给定整数![]() 及满足
及满足![]() 的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为
的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为![]() .
.
(1)证明:![]() ;
;
(2)若在图G中再添加一条边就存在k+1团,求图G的中心点个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月,台风“山竹”在我国多个省市登陆,造成直接经济损失达52亿元.某青年志愿者组织调查了某地区的50个农户在该次台风中造成的直接经济损失,将收集的数据分成五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元),得到如图所示的频率分布直方图.
(单位:元),得到如图所示的频率分布直方图.
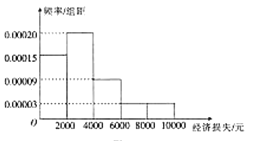
(1)试根据频率分布直方图估计该地区每个农户的平均损失(同一组中的数据用该组区间的中点值代表);
(2)台风后该青年志愿者与当地政府向社会发出倡议,为该地区的农户捐款帮扶,现从这50户并且损失超过4000元的农户中随机抽取2户进行重点帮扶,设抽出损失超过8000元的农户数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”的大意是凑够一撮人即可走,跟红绿灯无关.部分法律专家的观点为“交通规则的制定目的就在于服务城市管理,方便行人,而‘中国式过马路’是对我国法治化进程的严重阻碍,反应了国人规则意识的淡薄.”某新闻媒体对此观点进行了网上调查,所有参与调查的人中,持“支持”“中立”和“不支持”态度的人数如表所示:
支持 | 中立 | 不支持 | |
20岁以下 | 700 | 450 | 200 |
20岁及以上 | 200 | 150 | 300 |
在所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,则持“支持”态度的人中20岁及以上的有_________人
人,则持“支持”态度的人中20岁及以上的有_________人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为![]() 和
和![]() ,现安排甲组研发新产品
,现安排甲组研发新产品![]() ,乙组研发新产品
,乙组研发新产品![]() .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品![]() 研发成功,预计企业可获得
研发成功,预计企业可获得![]() 万元,若新产品
万元,若新产品![]() 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润![]() 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强学生体质,合肥一中组织体育社团,某班级有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团.
(1)求这4人中恰有1人参加篮球社团的概率;
(2)用![]() ,
,![]() 分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为
分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为![]() 和
和![]() 之差的绝对值,求随机变量X的分布列与数学期望
之差的绝对值,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com