
【题目】(1)设a,b是两个不相等的正数,若![]() ,用综合法证明:a+b>4
,用综合法证明:a+b>4
(2)已知a>b>c,且a+b+c=0,用分析法证明:![]() .
.
【答案】(1)详见解析(2)详见解析
【解析】试题分析:(1)综合法,从已知条件出发,利用定义、公理、定理、性质等,经过一系列的推理,论证而得出命题成立,这种证明方法称为综合法即“由因寻果”的方法;(2)分析法,从所要证明的结论出发,逐步寻求使它成立的充分条件,直至所需条件为已知条件或一个明显成立的事实,从而得出要证的命题成立,这种证明方法称为分析法,即“执果索因”的证明方法.
试题解析:(1)因为a>0,b>0,且a≠b,
所以a+b=(a+b)(![]() )=1+1+
)=1+1+![]() >2+2
>2+2![]() =4.所以a+b>4
=4.所以a+b>4
(2)因为a>b>c,且a+b+c=0,所以a>0,c<0,
要证明原不等式成立,只需证明![]()
即证b2-ac<3a2,又b=-(a+c),从而只需证明(a+c)2-ac<3a2,
即证(a-c)(2a+c)>0,
因为a-c>0,2a+c=a+c+a=a-b>0,
所以(a-c)(2a+c)>0成立,故原不等式成立.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】已知点(0,1),(3+2![]() ,0),(3-2
,0),(3-2![]() ,0)在圆C上.
,0)在圆C上.
(1)求圆C的方程.
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是双曲线![]()
![]() 左支上一点,
左支上一点, ![]() 是双曲线的左右两个焦点,且
是双曲线的左右两个焦点,且![]() ,线段
,线段![]() 的垂直平分线恰好是该双曲线的一条渐近线,则离心率为( )
的垂直平分线恰好是该双曲线的一条渐近线,则离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应阳光体育运动的号召,某县中学生足球活动正如火如荼地展开,该县为了解本县中学生的足球运动状况,根据性别采取分层抽样的方法从全县24000名中学生(其中男生14000人,女生10000人)中抽取120名,统计他们平均每天足球运动的时间,如下表:(平均每天足球运动的时间单位为小时,该县中学生平均每天足球运动的时间范围是![]() ).
).
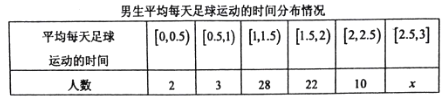
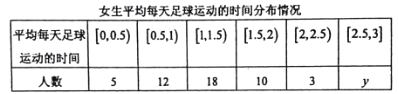
(1)请根据样本估算该校男生平均每天足球运动的时间(结果精确到0.1);
(2)若称平均每天足球运动的时间不少于2小时的学生为“足球健将”,低于2小时的学生为“非足球健将”.
①请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断,能否有90%的把握认为是否为“足球健将”与性别有关?
列联表,并通过计算判断,能否有90%的把握认为是否为“足球健将”与性别有关?
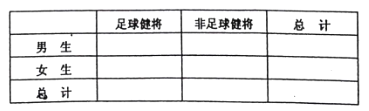
②若在足球运动时间不足1小时的男生中抽取2名代表了解情况,求这2名代表都是足球运动时间不足半小时的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.05 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 3.841 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)当![]() 时,若对任意互不相等的实数
时,若对任意互不相等的实数![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)判断函数![]() 在
在![]() 上的零点的个数,并说明理由.
上的零点的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(λx+1)ln x-x+1.
(1)若λ=0,求f(x)的最大值;
(2)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,证明:![]() >0.
>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校高三学生的视力情况,随机地抽查了该校1000名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为![]() ,视力在4.6到5.0之间的学生数
,视力在4.6到5.0之间的学生数![]() ,
, ![]() 的值分别为( )
的值分别为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com