
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点
的中点

(1)证明:![]() ;
;
(2)若![]() 为棱
为棱![]() 上一点,满足
上一点,满足![]() ,求锐二面角
,求锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见详解;(2)![]()
【解析】
(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法证明![]() ;
;
(2)设![]() ,由
,由![]() ,求出
,求出![]() ,求出平面ABF的法向量和平面ABP的法向量,利用向量法能求出二面角
,求出平面ABF的法向量和平面ABP的法向量,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
证明:(1)∵在四棱锥PABCD中,PA⊥底面ABCD,AD⊥AB,
AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
∴以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
B(1,0,0),P(0,0,2),C(2,2,0),E(1,1,1),D(0,2,0),![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;
(2)∵F为棱PC上一点,满足![]() ,
,
∴设![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
∵![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
设平面ABF的法向量![]() ,
,
则 ,取
,取![]() ,得
,得![]() ,
,
平面ABP的一个法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】药材人工种植技术具有养殖密度高、经济效益好的特点.研究表明:人工种植药材时,某种药材在一定的条件下,每株药材的年平均生长量![]() 单位:千克
单位:千克![]() 是每平方米种植株数x的函数.当x不超过4时,v的值为2;当
是每平方米种植株数x的函数.当x不超过4时,v的值为2;当![]() 时,v是x的一次函数,其中当x为10时,v的值为4;当x为20时,v的值为0.
时,v是x的一次函数,其中当x为10时,v的值为4;当x为20时,v的值为0.
![]() 当
当![]() 时,求函数v关于x的函数表达式;
时,求函数v关于x的函数表达式;
![]() 当每平方米种植株数x为何值时,每平方米药材的年生长总量
当每平方米种植株数x为何值时,每平方米药材的年生长总量![]() 单位:千克
单位:千克![]() 取得最大值?并求出这个最大值.
取得最大值?并求出这个最大值.![]() 年生长总量
年生长总量![]() 年平均生长量
年平均生长量![]() 种植株数
种植株数![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“文、明、中、国”四个字,有放回地从中任取一个小球,直到“中”“国”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“文、明、中、国”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 013 320 122 103 233
由此可以估计,恰好第三次就停止的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过4(尾/立方米)时,
不超过4(尾/立方米)时,![]() 的值为
的值为![]() (千克/年);当
(千克/年);当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 达到
达到![]() (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因,![]() 的值为
的值为![]() (千克/年).
(千克/年).
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当养殖密度![]() 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中所有正确命题的序号是__________.
①抛物线![]() 的准线方程为
的准线方程为![]() ;
;
②过点![]() 作与抛物线
作与抛物线![]() 只有一个公共点的直线
只有一个公共点的直线![]() 仅有1条;
仅有1条;
③![]() 是抛物线
是抛物线![]() 上一动点,以
上一动点,以![]() 为圆心作与抛物线准线相切的圆,则此圆一定过定点
为圆心作与抛物线准线相切的圆,则此圆一定过定点![]() .
.
④抛物线![]() 上到直线
上到直线![]() 距离最短的点的坐标为
距离最短的点的坐标为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统综》中有这样的一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”.其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,请问此人第2天走的路程为
A. 24里 B. 48里 C. 72里 D. 96里
查看答案和解析>>
科目:高中数学 来源: 题型:
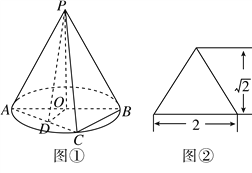
【题目】圆锥![]() 如图①所示,图②是它的正(主)视图.已知圆
如图①所示,图②是它的正(主)视图.已知圆![]() 的直径为
的直径为![]() ,
, ![]() 是圆周上异于
是圆周上异于![]() 的一点,
的一点, ![]() 为
为![]() 的中点.
的中点.
(I)求该圆锥的侧面积S;
(II)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(III)若∠CAB=60°,在三棱锥![]() 中,求点
中,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com