
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)在第(2)问的条件下,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就2015年毕业大学生的月收入情况调查了10000人,并根据所得数据画出样本的频率分布直方图所示,每个分组包括左端点,不包括右端点,如第一组表示![]() .
.
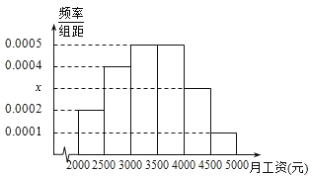
(1)求毕业大学生月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析大学生的收入与所学专业、性别等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽取多少人?
的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并与圆
外切并与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若双曲线![]() 的右焦点即为曲线
的右焦点即为曲线![]() 的右顶点,直线
的右顶点,直线![]() 为
为![]() 的一条渐近线.
的一条渐近线.
①.求双曲线C的方程;
②.过点![]() 的直线
的直线![]() ,交双曲线
,交双曲线![]() 于
于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点(
点(![]() 点与
点与![]() 的顶点不重合),当
的顶点不重合),当![]() ,且
,且![]() 时,求
时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=1,AD=![]() 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
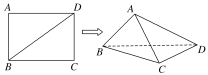
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了![]() ,
, ![]() ,
, ![]() ,
, ![]() 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是![]() ,3号门里是
,3号门里是![]() ;乙同学说:2号门里是
;乙同学说:2号门里是![]() ,3号门里是
,3号门里是![]() ;丙同学说:4号门里是
;丙同学说:4号门里是![]() ,2号门里是
,2号门里是![]() ;丁同学说:4号门里是
;丁同学说:4号门里是![]() ,3号门里是
,3号门里是![]() .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com