
【题目】已知偶函数![]() 满足
满足![]() ,现给出下列命题:①函数
,现给出下列命题:①函数![]() 是以2为周期的周期函数;②函数
是以2为周期的周期函数;②函数![]() 是以4为周期的周期函数;③函数
是以4为周期的周期函数;③函数![]() 为奇函数;④函数
为奇函数;④函数![]() 为偶函数,则其中真命题的个数是( )
为偶函数,则其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
由偶函数的定义和条件,将x换为x+2,可得f(x+4)=f(x),可得周期为4,即可判断①②的正确性;再由奇函数、偶函数的定义,将x换为﹣x,化简变形即可判断③④的正确性.
解:偶函数f(x)满足f(x)+f(2﹣x)=0,
即有f(﹣x)=f(x)=﹣f(2﹣x),
即为f(x+2)=﹣f(x),f(x+4)=﹣f(x+2)=f(x),
可得f(x)的最小正周期为4,故①错误;②正确;
由f(x+2)=﹣f(x),可得f(x+1)=﹣f(x﹣1),
又f(﹣x﹣1)=f(x+1),即有f(﹣x﹣1)=﹣f(x﹣1),故f(x﹣1)为奇函数,故③正确;
由f(﹣x﹣3)=f(x+3),若f(x﹣3)为偶函数,即有f(﹣x﹣3)=f(x﹣3),
可得f(x+3)=f(x﹣3),即f(x+6)=f(x),可得6为f(x)的周期,这与4为最小正周期矛盾,故④错误.
故选:B.


科目:高中数学 来源: 题型:
【题目】如图,A 为椭圆![]() 的下顶点,过 A 的直线 l 交抛物线
的下顶点,过 A 的直线 l 交抛物线![]() 于B、C 两点,C 是 AB 的中点.
于B、C 两点,C 是 AB 的中点.
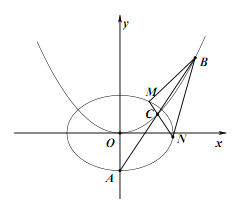
(I)求证:点C的纵坐标是定值;
(II)过点C作与直线 l 倾斜角互补的直线l交椭圆于M、N两点,求p的值,使得△BMN的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上的点到焦点的最长距离为
,且椭圆上的点到焦点的最长距离为![]() .
.
(1)求椭圆C的方程;
(2)过点P(0,2)的直线l(不过原点O)与椭圆C交于两点A、B,M为线段AB的中点.
(ⅰ)证明:直线OM与l的斜率乘积为定值;
(ⅱ)求△OAB面积的最大值及此时l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5G网络是第五代移动通信网络,其峰值理论传输速度可达每8秒1GB,比4G网络的传输速度快数百倍.举例来说,一部1G的电影可在8秒之内下载完成.随着5G技术的诞生,用智能终端分享3D电影、游戏以及超高画质(UHD)节目的时代正向我们走来.某手机网络研发公司成立一个专业技术研发团队解决各种技术问题,其中有数学专业毕业,物理专业毕业,其它专业毕业的各类研发人员共计1200人.现在公司为提高研发水平,采用分层抽样抽取400人按分数对工作成绩进行考核,并整理得如上频率分布直方图(每组的频率视为概率).

(1)从总体的1200名学生中随机抽取1人,估计其分数小于50的概率;
(2)研发公司决定对达到某分数以上的研发人员进行奖励,要求奖励研发人员的人数达到30%,请你估计这个分数的值;
(3)已知样本中有三分之二的数学专业毕业的研发人员分数不低于70分,样本中不低于70分的数学专业毕业的研发人员人数与物理及其它专业毕业的研发人员的人数和相等,估计总体中数学专业毕业的研发人员的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2017年,大连“蜗享出行”正式引领共享汽车,改变人们传统的出行理念,给市民出行带来了诸多便利![]() 该公司购买了一批汽车投放到市场给市民使用
该公司购买了一批汽车投放到市场给市民使用![]() 据市场分析,每辆汽车的营运累计收入
据市场分析,每辆汽车的营运累计收入![]() 单位:元
单位:元![]() 与营运天数
与营运天数![]() 满足
满足![]() .
.
![]() 要使营运累计收入高于1400元求营运天数的取值范围;
要使营运累计收入高于1400元求营运天数的取值范围;
![]() 每辆汽车营运多少天时,才能使每天的平均营运收入最大?
每辆汽车营运多少天时,才能使每天的平均营运收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已两动圆![]() 和
和![]()
![]() ,把它们的公共点的轨迹记为曲线
,把它们的公共点的轨迹记为曲线![]() ,若曲线
,若曲线![]() 与
与![]() 轴的正半轴交点为
轴的正半轴交点为![]() ,且曲线
,且曲线![]() 上异于点
上异于点![]() 的相异两点
的相异两点![]() 、
、![]() 满足
满足![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)证明直线![]() 恒经过一定点,并求出此定点的坐标.
恒经过一定点,并求出此定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系(
轴正半轴为极轴,建立极坐标系(![]() ),点
),点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() 。
。
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)设点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 面积的最小值。
面积的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com