
【题目】已知A(4,-3),B(2,-1)和直线l:4x+3y-2=0.
(1)求在直角坐标平面内满足|PA|=|PB|的点P的方程;
(2)求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由题意可知|PA|=|PB|即点P为线段AB的中垂线,所过点P的轨迹为过AB中点,斜率满足![]() 。(2)由(1)可知点P的方程x-y-5=0,
。(2)由(1)可知点P的方程x-y-5=0,
设点P的坐标为(a,b),再由点到直线的距离公式和点在直线x-y-5=0,列方程组可解。
试题解析:(1)∵A(4,-3),B(2,-1),
∴线段AB的中点M的坐标为(3,-2),又![]()
∴线段AB的垂直平分线方程为y+2=x-3,
即点P的方程x-y-5=0.
(2)设点P的坐标为(a,b),
∵点P(a,b)在上述直线上,∴a-b-5=0.①
又点P(a,b)到直线l:4x+3y-2=0的距离为2,
∴![]() =2,即4a+3b-2=±10,②
=2,即4a+3b-2=±10,②
联立①②可得![]() 或
或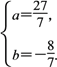
∴所求点P的坐标为(1,-4)或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)在(2)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:某污水处理厂要在一个矩形污水处理池(![]() )的池底水平铺设污水净化管道(
)的池底水平铺设污水净化管道(![]() 是直角顶点)来处理污水,管道越长污水净化效果越好,设计要求管道的的接口
是直角顶点)来处理污水,管道越长污水净化效果越好,设计要求管道的的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上。已知
上。已知![]() 米,
米,![]() 米,记
米,记![]() .
.
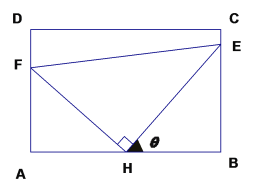
(1)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(3)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度。
取何值时,污水净化效果最好?并求出此时管道的长度。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
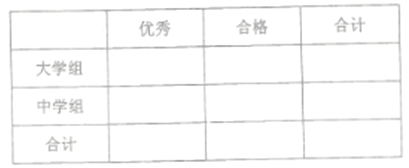


(2)若参赛选手共6万人,用频率估计概率,试估计其中优秀等级的选手人数;
(3)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6,在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为![]() ,在选出的6名良好等级的选手中任取一名,记其编号为
,在选出的6名良好等级的选手中任取一名,记其编号为![]() ,求使得方程组
,求使得方程组![]() 有唯一一组实数解
有唯一一组实数解![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学参加科普知识竞赛,需回答3个问题,竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分,假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.
(1)求这名同学得300分的概率;
(2)求这名同学至少得300分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称![]() )是定量描述空气质量状况的指数,空气质量按照
)是定量描述空气质量状况的指数,空气质量按照![]() 大小分为六级,
大小分为六级,![]() 为优;
为优;![]() 为轻度污染;
为轻度污染;![]() 为中度污染;
为中度污染;![]() 为重度污染;
为重度污染;![]() 为严重污染.一环保人士记录去年某地某月10天的
为严重污染.一环保人士记录去年某地某月10天的![]() 的茎叶图如右.
的茎叶图如右.
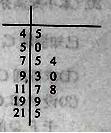
(1)利用该样本估计该地本月空气质量优良(![]() )的天数;(按这个月总共30天计算)
)的天数;(按这个月总共30天计算)
(2)将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为![]() ,求
,求![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于空间直角坐标系![]() 中的一点
中的一点![]() ,有下列说法:
,有下列说法:
①点![]() 到坐标原点的距离为
到坐标原点的距离为![]() ;
;
②![]() 的中点坐标为
的中点坐标为![]() ;
;
③点![]() 关于
关于![]() 轴对称的点的坐标为
轴对称的点的坐标为![]() ;
;
④点![]() 关于坐标原点对称的点的坐标为
关于坐标原点对称的点的坐标为![]() ;
;
⑤点![]() 关于坐标平面
关于坐标平面![]() 对称的点的坐标为
对称的点的坐标为![]() .
.
其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究性学习中,关于三角形与三角函数知识的应用(约定三内角![]() 所对的边分别是
所对的边分别是![]() )得出如下一些结论:
)得出如下一些结论:
(1)若![]() 是钝角三角形,则
是钝角三角形,则![]() ;
;
(2)若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
(3)在三角形![]() 中,若
中,若![]() ,则
,则![]()
(4)在![]() 中,若
中,若![]() ,则
,则![]()
其中错误命题的个数是 ( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com