
����Ŀ����֪����M={��x��y��|y=f��x��}������������ʵ���ԣ�x1 �� y1����M�����ڣ�x2 �� y2����M��ʹx1x2+y1y2=0��������Ƽ���M�ǡ���ֱ�Ե㼯�������������ĸ����ϣ� ��M={��x��y��|y= ![]() }��
}��
��M={��x��y��|y=log2x}��
��M={��x��y��|y=2x��2}��
��M={��x��y��|y=sinx+1}��
�����ǡ���ֱ�Ե㼯��������ǣ� ��
A.�٢ڢ�
B.�٢ڢ�
C.�٢ۢ�
D.�ڢۢ�
���𰸡�C
���������⣺������ɵã�����M�ǡ���ֱ�Ե㼯���������㣺 ����y=f��x���Ϲ�����һ����ԭ���ֱ�ߣ������ڹ���һ����ԭ���ֱ����֮��ֱ��
��M={��x��y��|y= ![]() }����ͼ���������Һ�x�����ӽ������Ϻ�y�����ӽ���
}����ͼ���������Һ�x�����ӽ������Ϻ�y�����ӽ���
���ݺ�����ͼ������ʿ�֪��
��ͼ������ȡһ��A����OA����ԭ����OA�Ĵ���OB����y= ![]() ��ͼ���ཻ��
��ͼ���ཻ��
��һ�����ڵ�B��ʹ��OB��OA������
��M={��x��y��|y= ![]() }�ǡ���ֱ�Ե㼯����
}�ǡ���ֱ�Ե㼯����
��M={��x��y��|y=log2x}����x��0����
ȡ��1��0�������ڵ㣨x2 �� log2x2����x2��0��������1��x2+0=0��
��˼���M���ǡ���ֱ�Ե㼯����
���ڢ�M={��x��y��|y=2x��2}����ͼ����㣨0����1��������������������չ����������������չ��
��ָ��������ͼ������ʿ�֪��
��ͼ������ȡһ��A����OA����ԭ����OA�Ĵ���OB����y=2x��2��ͼ���ཻ��
��һ�����ڵ�B��ʹ��OB��OA������
��M={��x��y��|y=2x��2}�ǡ���ֱ�Ե㼯����
���ڢ�M={��x��y��|y=sinx+1}����ͼ������ȡһ��A��
��OA����ԭ����ֱ��OA�Ĵ���OB����Ϊy=sinx+1��ͼ����x����������������չ������x�����У�
���ֱ��OB�ܻ���y=sinx+1��ͼ���ཻ��
����M={��x��y��|y=sinx+1}�ǡ���ֱ�Ե㼯�����ʢܷ��ϣ�
���Ͽɵã�ֻ�Т٢ۢ��ǡ���ֱ�Ե㼯����
��ѡ��C
�����㾫�����������������ж���Ӧ���ǽ����ĸ�������Ҫ֪���������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016���й�(��������)���������������������������ֵĴ���֧���£�Բ��˳������.��֯��ͳ�������� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��ӵ����ӵ�ƽ�������뱾�α�����ƽ���÷֣����±���ʾ��
��ӵ����ӵ�ƽ�������뱾�α�����ƽ���÷֣����±���ʾ��
��� |
|
|
|
|
|
ƽ������ | 170 | 174 | 176 | 181 | 179 |
ƽ���÷� | 62 | 64 | 66 | 70 | 68 |
��1�����ݱ������ݣ��� ![]() ����
���� ![]() �����Իع鷽�̣�ϵ����ȷ��
�����Իع鷽�̣�ϵ����ȷ�� ![]() ����
����
��2���� ![]() ��ƽ������Ϊ
��ƽ������Ϊ ![]()
![]() �����ݣ�1��������õĻع鷽�̣�Ԥ��
�����ݣ�1��������õĻع鷽�̣�Ԥ�� ![]() �ӵ�ƽ���÷�.����ȷ����λ�� ע���ع鷽��
�ӵ�ƽ���÷�.����ȷ����λ�� ע���ع鷽�� ![]() ��б�ʺͽؾ���С���˹��ƹ�ʽ�ֱ�Ϊ
��б�ʺͽؾ���С���˹��ƹ�ʽ�ֱ�Ϊ ��
�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A1 �� A2Ϊ��Բ ![]() =1�ij�������Ҷ˵㣬OΪ����ԭ�㣬S��Q��TΪ��Բ�ϲ�ͬ��A1 �� A2�����㣬ֱ��QA1 �� QA2 �� OS��OTΧ��һ��ƽ���ı���OPQR����|OS|2+|OT|2=�� ��
=1�ij�������Ҷ˵㣬OΪ����ԭ�㣬S��Q��TΪ��Բ�ϲ�ͬ��A1 �� A2�����㣬ֱ��QA1 �� QA2 �� OS��OTΧ��һ��ƽ���ı���OPQR����|OS|2+|OT|2=�� �� 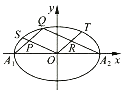
A.5
B.3+ ![]()
C.9
D.14
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽������ڹ���ʳ��ʱ��Ӫ��˵�����Ա�Ĺ�ϵ��������������ѯ����100�����õ�����2��2��������
��1���Ƿ���95%�İ�����Ϊ�����Ա����Ӫ��˵���й�ϵ������˵�����ɣ�
��2����Ƶ�ʵ����ʣ���������ϵ����������������ȡ3λ������3λ�ж�Ӫ��˵��������Ϊ�Σ�����������εķֲ��к���ѧ����E���Σ���
���� | Ů�� | �ܼ� | |
��Ӫ��˵�� | 40 | 20 | 60 |
����Ӫ��˵�� | 20 | 20 | 40 |
�ܼ� | 60 | 40 | 100 |
�ο���ʽ�����ݣ� ![]()
P��K2��k0�� | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����F��x��= ![]() ����aΪʵ������
����aΪʵ������
��1������a�IJ�ͬȡֵ�����ۺ���y=f��x������ż�ԣ���˵�����ɣ�
��2�����������x��1������1��f��x����3����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��F1 �� F2�ֱ�����ԲC�� ![]() =1��a��b��0�������ҽ��㣬�ҽ���Ϊ2
=1��a��b��0�������ҽ��㣬�ҽ���Ϊ2 ![]() ������ABƽ����x�ᣬ��|F1A|+|F1B|=4��
������ABƽ����x�ᣬ��|F1A|+|F1B|=4��
��1������ԲC�ķ��̣�
��2������P����ԲC�����ڵ� ![]() ��A��B������һ�㣬��ֱ��PA��PB�ֱ���y�ύ�ڵ�M��N����MF2��NF2��б�ʷֱ�Ϊk1��k2 �� ��֤��k1k2�Ƕ�ֵ��
��A��B������һ�㣬��ֱ��PA��PB�ֱ���y�ύ�ڵ�M��N����MF2��NF2��б�ʷֱ�Ϊk1��k2 �� ��֤��k1k2�Ƕ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��Ma={f��x��|������ʵ��a��ʹ�ö�����������x����f��x+a����f��x��}��
��1����f��x��=2x��x2 �� ���ж�f��x���Ƿ�ΪM1�е�Ԫ�أ���˵�����ɣ�
��2���� ![]() ����g��x����Ma �� ��a��ȡֵ��Χ��
����g��x����Ma �� ��a��ȡֵ��Χ��
��3���� ![]() ��k��R������h��x����M2 �� ��h��x������Сֵ��
��k��R������h��x����M2 �� ��h��x������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ԲC������Ϊԭ��O��F����2 ![]() ��0��ΪC���㣬PΪC��һ�㣬����|OP|=|OF|��|PF|=4������ԲC�ķ���Ϊ�� ��
��0��ΪC���㣬PΪC��һ�㣬����|OP|=|OF|��|PF|=4������ԲC�ķ���Ϊ�� �� 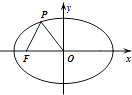
A.![]() =1
=1
B.![]() =1
=1
C.![]() =1
=1
D.![]() =1
=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABC�У�AB=AC=PB=PC=10��PA=8��BC=12����M��ƽ��PBC�ڣ���AM=7��������ֱ��AM��BC���ɽ�Ϊ������cos�������ֵΪ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com