
| OB |
| OC |
| OB |
| OC |
| OA |
| OA |
| OB |
| OC |
| OB |
| OC |
| OB |
| OC |
| OA |
| OB |
| OC |
| OB |
| OA |
| OC |
| OA |
| OB |
| OC |
| AB |
| AC |
| CB |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源:江苏省南通市通州区2012届高三4月查漏补缺专项检测数学试题 题型:022
已知△ABC中,∠B=60°,O为△ABC的外心,若点P在△ABC所在的平面上,![]() =
=![]() +
+![]() +
+![]() ,且
,且![]() ·
·![]() =8,则边AC上的高h的最大值为________.
=8,则边AC上的高h的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省常州中学高三最后冲刺综合练习数学试卷6(文科)(解析版) 题型:解答题
 =
=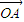 +
+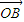 +
+ ,且
,且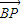 •
•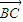 =8,则边AC上的高h的最大值为 .
=8,则边AC上的高h的最大值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com