
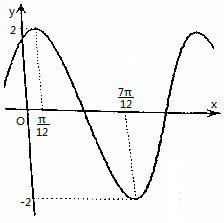
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图.分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)根据函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式.
(3)利用正弦函数的定义域和值域,分类讨论a的符号,从而求得实数a,b的值.
解答 解:(1)根据函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象,
可得A=2,$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{7π}{12}$-$\frac{π}{12}$,∴ω=2,再根据五点法作图可得2•$\frac{π}{12}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{3}$,
∴f(x)=2sin(2x+$\frac{π}{3}$).
(2)若g(x)的图象是将f(x)的图象向右平移$\frac{π}{24}$个单位得到的,
∴g(x)=f(x-$\frac{π}{24}$)=2sin[2(x-$\frac{π}{24}$)+$\frac{π}{3}$]=2sin(2x+$\frac{π}{4}$).
(3)∵h(x)=$\frac{\sqrt{2}}{4}$a•g(x)+$\frac{a}{2}$+b=$\frac{\sqrt{2}}{2}$asin(2x+$\frac{π}{4}$)+$\frac{a}{2}$+b,当x∈[0,$\frac{π}{2}$]时,2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],
若a>0,则当2x+$\frac{π}{4}$=$\frac{5π}{4}$时,h(x)取得最小值为$\frac{\sqrt{2}}{2}a$•(-$\frac{\sqrt{2}}{2}$)+$\frac{a}{2}$+b=3;
当2x+$\frac{π}{4}$=$\frac{π}{2}$时,h(x)取得最大值为$\frac{\sqrt{2}}{2}a$+$\frac{a}{2}$+b=4,求得a=2$\sqrt{2}$-2,b=3.
若a<0,则当2x+$\frac{π}{4}$=$\frac{5π}{4}$时,h(x)取得最大值为$\frac{\sqrt{2}}{2}a$•(-$\frac{\sqrt{2}}{2}$)+$\frac{a}{2}$+b=4;
当2x+$\frac{π}{4}$=$\frac{π}{2}$时,h(x)取得最小值为$\frac{\sqrt{2}}{2}a$+$\frac{a}{2}$+b=3,求得a=-2$\sqrt{2}$-2,b=4.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于中档题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | $(-∞,-\frac{7}{2}]$ | C. | $[-\frac{7}{2},-1)$ | D. | $[-\frac{7}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 把函数f(x)图象上各点的横坐标缩短到原来的一半(纵坐标不变),再向右平移$\frac{π}{4}$个单位长度,可得到函数g(x)的图象 | |
| B. | 两个函数的图象均关于直线x-=-$\frac{π}{4}$对称 | |
| C. | 两个函数在区间(-$\frac{π}{4}$,$\frac{π}{4}$)上都是单调递增函数 | |
| D. | 函数y=g(x)在[0,2π]上只有4个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log3x+4logx3 | B. | y=ex+4e-x | ||
| C. | y=sinx+$\frac{4}{sinx}$(0<x<π) | D. | y=x+$\frac{4}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com