
【题目】已知![]() ,函数
,函数![]() .
.
(Ⅰ)若![]() 有极小值且极小值为0 ,求
有极小值且极小值为0 ,求![]() 的值;
的值;
(Ⅱ)当![]() 时,
时,![]() , 求
, 求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】试题分析:(1)先求导数![]() ,再根据a的正负讨论导函数零点情况,当
,再根据a的正负讨论导函数零点情况,当![]() 时只有一个零点,且为极小值,再根据极小值为0 ,求
时只有一个零点,且为极小值,再根据极小值为0 ,求![]() 的值;当
的值;当![]() 时讨论两个零点大小,先确定极小值取法,再根据极小值为0 ,求
时讨论两个零点大小,先确定极小值取法,再根据极小值为0 ,求![]() 的值;(2)先化简不等式为
的值;(2)先化简不等式为![]() ,再对
,再对![]() 时,变量分离,转化为讨论对应函数最值问题
时,变量分离,转化为讨论对应函数最值问题![]() 最小值,先根据
最小值,先根据![]() 与
与![]() 同号得
同号得![]() >0,再根据放缩证明
>0,再根据放缩证明![]() 最小值恒大于零且趋于零,综合可得
最小值恒大于零且趋于零,综合可得![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)![]() .
.
①若![]() ,则由
,则由![]() 解得
解得![]() ,
,
当![]() 时,
时,![]() 递减;当
递减;当![]() 上,
上,![]() 递增;
递增;
故当![]() 时,
时,![]() 取极小值
取极小值![]() ,令
,令![]() ,得
,得![]() (舍去).
(舍去).
②若![]() ,则由
,则由![]() ,解得
,解得![]() .
.
(i)若![]() ,即
,即![]() 时,当
时,当![]() ,
,![]() .
.![]() 递增;当
递增;当![]() 上,
上,![]() 递减;当
递减;当![]() 上,
上,![]() 递增.
递增.
故当![]() 时,
时,![]() 取极小值
取极小值![]() ,令
,令![]() ,得
,得![]() (舍去)
(舍去)
(ii)若![]() ,即
,即![]() 时,
时,![]() 递增不存在极值;
递增不存在极值;
(iii)若![]() ,即
,即![]() 时,当
时,当![]() 上,
上,![]() 递增;
递增;![]() ,
,![]() 上,
上,![]() 递减;当
递减;当![]() 上,
上,![]() 递增.
递增.
故当![]() 时,
时,![]() 取极小值
取极小值![]() ,得
,得![]() 满足条件.
满足条件.
故当![]() 有极小值且极小值为0时,
有极小值且极小值为0时,![]()
(Ⅱ)方法一:![]() 等价于
等价于![]() ,
,
即![]() ,即
,即![]() ①
①
当![]() 时,①式恒成立;以下求当
时,①式恒成立;以下求当![]() 时不等式
时不等式![]() 恒成立,且当
恒成立,且当![]() 时不等式
时不等式![]() 恒成立时
恒成立时![]() 的取值范围.
的取值范围.
令![]() ,即
,即![]() ,记
,记![]() .
.
(i)当![]() 即
即![]() 时,
时,![]() 是
是![]() 上的增函数,
上的增函数,
所以![]() ,故当
,故当![]() 时,①式恒成立;
时,①式恒成立;
(ii)当![]() 即
即![]() 时,令
时,令![]() ,
,
若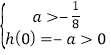 ,即
,即![]() 时,则
时,则![]() 在区间
在区间![]() 上有两个零点
上有两个零点![]() ,
,
其中![]() ,故
,故![]() 在
在![]() 上有两个零点:
上有两个零点:
![]() ,
,
在区间![]() 和
和![]() 上,
上,![]() 递增;在区间
递增;在区间![]() 上,
上,![]() 递减;
递减;
故在区间![]() 上,
上,![]() 取极大值
取极大值![]() , ②
, ②
注意到![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
注意到![]() ,在区间
,在区间![]() 上,
上,![]() 递增,所以
递增,所以![]() ,当
,当![]() 时,
时,![]() .
.
故当![]() 时,在区间
时,在区间![]() 上,
上,![]() ,而在区间
,而在区间![]() 上
上![]() .
.
当![]() 时,
时,![]() ,也满足当
,也满足当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故当![]() 时,①式恒成立;
时,①式恒成立;
(iii)若![]() ,则当
,则当![]() 时,
时,![]() ,即
,即![]() ,即当
,即当![]() 时,①式不可能恒成立.
时,①式不可能恒成立.
综上所述, 所求![]() 的取值范围是
的取值范围是![]() .
.
方法二:![]() 等价于
等价于![]() , ③
, ③
当![]() 时,③式恒成立;
时,③式恒成立;
当![]() 时,③式等价于:
时,③式等价于:![]() ,令
,令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,故当
,故当![]() 时,③式恒成立;
时,③式恒成立;
以下证明:对任意的正数![]() ,存在
,存在![]() ,使
,使![]() ,取
,取![]() ,则
,则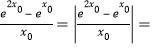
![]() ,令
,令![]() ,解得
,解得![]() ,即
,即![]() 时,
时,![]() ,
,
综上所述, 所求![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点相同,A为椭圆C的右顶点,以A为圆心的圆与直线
的焦点相同,A为椭圆C的右顶点,以A为圆心的圆与直线![]() 相交于P,
相交于P, ![]() 两点,且
两点,且![]()
(Ⅰ)求椭圆C的标准方程和圆A的方程;

(Ⅱ)不过原点的直线![]() 与椭圆C交于M、N两点,已知OM,直线
与椭圆C交于M、N两点,已知OM,直线![]() ,ON的斜率
,ON的斜率![]() 成等比数列,记以OM、ON为直径的圆的面积分别为S1、S2,试探究
成等比数列,记以OM、ON为直径的圆的面积分别为S1、S2,试探究![]() 的值是否为定值,若是,求出此值;若不是,说明理由.
的值是否为定值,若是,求出此值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,“一带一路”沿线的20国青年评选出了中国“新四大发明”:高铁、支付宝、共享单车和网购.2017年末,“支付宝大行动”用发红包的方法刺激支付宝的使用.某商家统计前5名顾客扫描红包所得金额分别为5.5元,2.1元,3.3元,5.9元,4.7元,商家从这5名顾客中随机抽取3人赠送台历.
(1)求获得台历的三人中至少有一人的红包超过5元的概率;
(2)统计一周内每天使用支付宝付款的人数![]() 与商家每天的净利润
与商家每天的净利润![]() 元,得到7组数据,如表所示,并作出了散点图.
元,得到7组数据,如表所示,并作出了散点图.

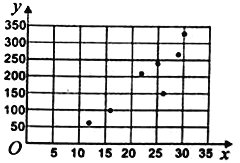
(i)直接根据散点图判断,![]() 与
与![]() 哪一个适合作为每天的净利润的回归方程类型.(
哪一个适合作为每天的净利润的回归方程类型.(![]() 的值取整数)
的值取整数)
(ii)根据(i)的判断,建立![]() 关于
关于![]() 的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
参考数据:
|
|
|
|
22.86 | 194.29 | 268.86 | 3484.29 |
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有编号为1,2,3,4,5的五个小球和编号为1,2,3,4,5的五个盒子,现将这五个小球放入5个盒子中.
(1)若没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(2)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计ABO血型具有民族和地区差异.在我国H省调查了30488人,四种血型的人数如下:
血型 | A | B | O | AB |
人数/人 | 7704 | 10765 | 8970 | 3049 |
频率 |
(1)计算H省各种血型的频率并填表(精确到0.001);
(2)如果从H省任意调查一个人的血型,那么他是O型血的概率大约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若f(x0)=x0,则称x0为f(x)的“不动点”,若f[f(x0)]=x0,则称x0为f(x)的“稳定点”,函数f(x)的“不动点”和“稳定点”的集合分别记为A和B,即A={x|f(x)=x},B={x|f[f(x)]=x},那么:
(1)函数g(x)=x2-2的“不动点”为______;
(2)集合A与集合B的关系是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三个顶点落在半径为
的三个顶点落在半径为![]() 的球
的球![]() 的表面上,三角形有一个角为
的表面上,三角形有一个角为![]() 且其对边长为3,球心
且其对边长为3,球心![]() 到
到![]() 所在的平面的距离恰好等于半径
所在的平面的距离恰好等于半径![]() 的一半,点
的一半,点![]() 为球面上任意一点,则
为球面上任意一点,则![]() 三棱锥的体积的最大值为( )
三棱锥的体积的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com