定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),
(1)求证:f(0)=1;
(2)求证:对任意的x∈R,恒有f(x)>0;
(3)已知f(x)是R上的增函数,若f(x)•f(2x-x2)>1,求x的取值范围.
解:(1)令a=b=0,则f(0)=[f(0)]
2
∵f(0)≠0
∴f(0)=1
(2)令a=x,b=-x,则 f(0)=f(x)f(-x)
∴f(-x)=
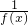
由已知x>0时,f(x)>1>0,
当x<0时,-x>0,f(-x)>0
∴f(x)=

>0
又x=0时,f(0)=1>0
∴对任意x∈R,f(x)>0
(3)f(x)•f(2x-x
2)=f[x+(2x-x
2)]=f(-x
2+3x)
又1=f(0),f(x)在R上递增
∴由f(3x-x
2)>f(0)
得:3x-x
2>0
∴0<x<3
分析:(1)令a=b=0,可由f(a+b)=f(a)f(b),求出f(0)=1;
(2)令a=x,b=-x,结合(1)中结论可得f(x)与f(-x)互为倒数,进而由已知可证得对任意的x∈R,恒有f(x)>0;
(3)根据(1)中结论,由已知将不等式f(x)•f(2x-x
2)>1,化为3x-x
2>0,易解得答案.
点评:本题考查的知识点是抽象函数及其应用,函数单调性的性质,函数恒成立问题,熟练掌握抽象函数“凑已知,凑未知”的解答技巧是关键.

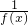
 >0
>0
