
已知数列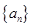 满足
满足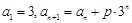 (
(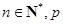 为常数),
为常数),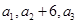 成等差数列.
成等差数列.
(Ⅰ)求p的值及数列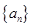 的通项公式;
的通项公式;
(Ⅱ)设数列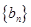 满足
满足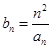 ,证明:
,证明: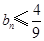 .
.
(Ⅰ)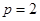 ,
, ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)利用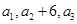 成等差数列.可求p的值,再用累加法求数列的通项公式;(Ⅱ)通过作差判断数列的单调性或利用数学归纳法进行证明.
成等差数列.可求p的值,再用累加法求数列的通项公式;(Ⅱ)通过作差判断数列的单调性或利用数学归纳法进行证明.
试题解析:(Ⅰ)由
得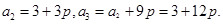
∵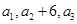 成等差数列,
成等差数列,
∴
即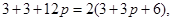 得
得 (2分)
(2分)
依题意知,
当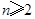 时,
时,
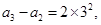

相加得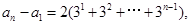
∴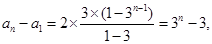
∴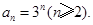 (4分)
(4分)
又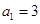 适合上式,
(5分)
适合上式,
(5分)
故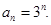 (6分)
(6分)
(Ⅱ)证明:∵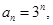 ∴
∴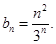
∵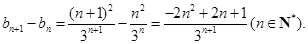 (8分)
(8分)
若 则
则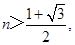
即当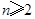 时,有
时,有 (10分)
(10分)
又因为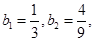 (11分)
(11分)
故 (12分)
(12分)
(Ⅱ)法二:要证
只要证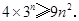 (7分)
(7分)
下面用数学归纳法证明:
①当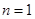 时,左边=12,右边=9,不等式成立;
时,左边=12,右边=9,不等式成立;
当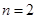 时,左边=36,右边=36,不等式成立.
(8分)
时,左边=36,右边=36,不等式成立.
(8分)
②假设当 时,
时,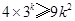 成立.
(9分)
成立.
(9分)
则当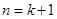 时,左边=4×3k+1=3×4×3k≥3×9k2,
时,左边=4×3k+1=3×4×3k≥3×9k2,
要证3×9k2≥9(k+1)2 ,
只要正3k2≥(k+1)2 ,
即证2k2-2k-1≥0. (10分)
而当k 即
即 且
且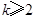 时,上述不等式成立. (11分)
时,上述不等式成立. (11分)
由①②可知,对任意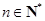 ,所证不等式成立.
(12分)
,所证不等式成立.
(12分)
考点:1.等差中项;2.累加法求和;3.数列单调性;4.数学归纳法.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com