练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设命题函数的值域为；命题，不等式恒成立，如果命题“”为真命题，且“”为假命题，求实数的取值范围。

    【答案】

    【解析】

    试题根据若命题“P或Q”为真命题，且“P且Q”为假命题知道P和Q一真一假，分两种情况进行讨论：P真Q假和P假Q真，再根据二次函数的恒成立问题的解法和不等式的恒成立问题的解法解题，要把每种情况都讨论清楚，不要遗漏知识点.

    试题解析：若命题“P或Q”为真命题，且“P且Q”为假命题，则有P和Q一真一假, .2分

    先求出P,Q都为真时a的取值：

    当P为真时，即对任意的，都有恒成立,

    则，解得, 4分

    当Q为真时，在区间上的最大值是3,

    则有恒成立，解得, 6分

    由上知当P,Q一真一假时有：

    P真Q假P假Q真, 10分

    解得. ...12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在原点，焦点在轴上，短轴长和焦距都等于2， 是椭圆上的一点，且在第一象限内，过且斜率等于的直线与椭圆交于另一点，点关于原点的对称点为.

    （Ⅰ）证明：直线的斜率为定值；

    （Ⅱ）求面积的最大值，并求此时直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）当时，求函数的极值；

    （2）设函数在处的切线方程为，若函数是上的单调增函数，求的值；

    （3）是否存在一条直线与函数的图象相切于两个不同的点？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】研究变量，得到一组样本数据，进行回归分析，有以下结论

    ①残差平方和越小的模型，拟合的效果越好；

    ②用相关指数来刻画回归效果，越小说明拟合效果越好；

    ③线性回归方程对应的直线至少经过其样本数据点中的一个点；

    ④若变量和之间的相关系数为，则变量和之间的负相关很强.

    以上正确说法的个数是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年5月27日当今世界围棋排名第一的柯洁在与的人机大战中中盘弃子认输，至此柯洁与的三场比赛全部结束，柯洁三战全负，这次人机大战再次引发全民对围棋的关注，某学校社团为调查学生学习围棋的情况，随机抽取了100名学生进行调查，根据调查结果绘制的学生日均学习围棋时间的频率分布直方图（如图所示），将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

    （1）请根据已知条件完成下面列联表，并据此资料你是否有95%的把握认为“围棋迷”与性别有关？

    非围棋迷

    围棋迷

    合计

    男

    女

    10

    55

    合计

    （2）为了进一步了解“围棋迷”的围棋水平，从“围棋迷”中按性别分层抽样抽取5名学生组队参加校际交流赛，首轮该校需派两名学生出赛，若从5名学生中随机抽取2人出赛，求2人恰好一男一女的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，用总长为定值l的篱笆围成长方形的场地，以墙为一边，并用平行于一边的篱笆隔开.

    （1）设场地面积为y，垂直于墙的边长为x，试用解析式将y表示成x的函数，并确定这个函数的定义域；

    （2）怎样围才能使得场地的面积最大?最大面积是多少?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，直线的参数方程为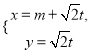（为参数），以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，且直线经过曲线的左焦点．

    （1）求的值及直线的普通方程；

    （2）设曲线的内接矩形的周长为，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地举办水果观光采摘节，并推出配套旅游项目，统计了4月份100名游客购买水果的情况，得到如图所示的频率分布直方图．

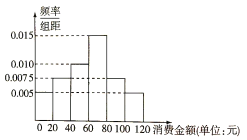
    （1）若将消费金额不低于80元的游客称为“水果达人”，现用分层抽样的方法从样本的“水果达人”中抽取5人，求这5人中消费金额不低于100元的人数；

    （2）从（1）中的5人中抽取2人作为幸运客户免费参加配套旅游项目，请列出所有的可能结果，并求这2人中至少有1人购买金额不低于100元的概率；

    （3）为吸引顾客，该地特推出两种促销方案，

    方案一：每满80元可立减8元；

    方案二：金额超过50元但又不超过80元的部分打9折，金额超过80元但又不超过100元的部分打8折，金额超过100元的部分打7折．

    若水果的价格为11元／千克，某游客要购买10千克，应该选择哪种方案.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，底面 是边长为1的正方形，平面，，与平面所成角为60°.

    （1）求证： 平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案