
 的图象与直线y=x至少有一个交点,求实数a的取值范围.
的图象与直线y=x至少有一个交点,求实数a的取值范围. ,令h(x)=ϕ(x)-x,由题意得h(x)=0在区间(0,+∞)上至少有一解,下面利用导数工具结合分类讨论思想研究此函数的单调性,最后综合得出a的取值范围.
,令h(x)=ϕ(x)-x,由题意得h(x)=0在区间(0,+∞)上至少有一解,下面利用导数工具结合分类讨论思想研究此函数的单调性,最后综合得出a的取值范围. ,∴g(x)的图象在x=2切线的斜率为:g′(2)=
,∴g(x)的图象在x=2切线的斜率为:g′(2)= ,
, ,∴a=-1,
,∴a=-1, -2≥2
-2≥2 -2>0
-2>0
 ,令h'(x)=0,得
,令h'(x)=0,得
 <0即a<0时,h(x)单调递增区间为(0,1),减区间为(1,+∞),
<0即a<0时,h(x)单调递增区间为(0,1),减区间为(1,+∞), >1即
>1即 时,h(x)单调递增区间为(0,1),(
时,h(x)单调递增区间为(0,1),( ,减区间为(1,
,减区间为(1, ),所以极大值h(1)=-1,极小值
),所以极大值h(1)=-1,极小值 ,
,
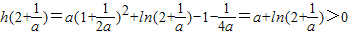 ,所以方程恰好有一解;
,所以方程恰好有一解; 时,h'(x)≥0,由上②知方程也恰好有一解;
时,h'(x)≥0,由上②知方程也恰好有一解; 时,h(x)单调递增区间为(0,
时,h(x)单调递增区间为(0, ),(1,+∞),减区间为(
),(1,+∞),减区间为( ,1),
,1),

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com