
已知函数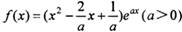
(1) 求曲线 在点A(0,
在点A(0, )处的切线方程;
)处的切线方程;
(2) 讨论函数 的单调性;
的单调性;
(3) 是否存在实数 ,使
,使 当
当 时恒成立?若存在,求出实数a;若不存在,请说明理由.
时恒成立?若存在,求出实数a;若不存在,请说明理由.
(1)∵ a>0,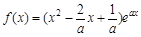 ,
,
∴ 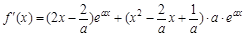
= ,
…………… 2分
,
…………… 2分
于是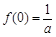 ,
,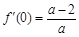 ,所以曲线y = f(x)在点A(0,f(0))处的切线方程为
,所以曲线y = f(x)在点A(0,f(0))处的切线方程为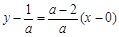 ,即(a-2)x-ay + 1 = 0.
… 4分
,即(a-2)x-ay + 1 = 0.
… 4分
(2)∵ a>0,eax>0,∴ 只需讨论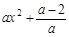 的符号.
………… 5分
的符号.
………… 5分
ⅰ)当a>2时,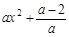 >0,这时f ′(x)>0,所以函数f(x)在(-∞,+∞)上为增函数.
>0,这时f ′(x)>0,所以函数f(x)在(-∞,+∞)上为增函数.
ⅱ)当a = 2时,f ′(x)= 2x2e2x≥0,函数f(x)在(-∞,+∞)上为增函数.
ⅲ)当0<a<2时,令f ′(x)= 0,解得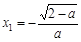 ,
,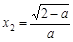 .
.
当x变化时, f '(x)和f(x)的变化情况如下表:
|
x |
|
|
|
|
|
|
f '(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
∴ f(x)在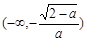 ,
,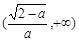 为增函数,
为增函数,
f(x)在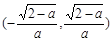 为减函数.
为减函数.
(3)当a∈(1,2)时,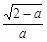 ∈(0,1).由(2)知f(x)在
∈(0,1).由(2)知f(x)在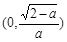 上是减函数,在
上是减函数,在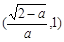 上是增函数,故当x∈(0,1)时,
上是增函数,故当x∈(0,1)时,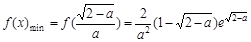 ,所以
,所以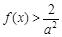 当x∈(0,1)时恒成立,等价于
当x∈(0,1)时恒成立,等价于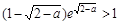 恒成立.当a∈(1,2)时,
恒成立.当a∈(1,2)时,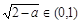 ,设
,设 ,则
,则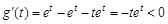 ,表明g(t)
在(0,1)上单调递减,于是可得
,表明g(t)
在(0,1)上单调递减,于是可得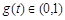 ,即a∈(1,2)时
,即a∈(1,2)时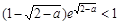 恒成立,因此,符合条件的实数a不存在.
恒成立,因此,符合条件的实数a不存在.
【解析】略


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:高中数学 来源:2013-2014学年广东省高三上学期第二次段考文科数学试卷(解析版) 题型:解答题
已知函数 ,
, .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省铁岭市六校协作高三第一次联合考试理科数学试卷(解析版) 题型:解答题
已知函数
(1)求函数 的最小正周期.
的最小正周期.
(2)当 时,求函数
时,求函数 的单调减区间.
的单调减区间.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三10月份月考理科数学试卷 题型:解答题
已知函数 .
(1) 求函数
.
(1) 求函数 的定义域;(2) 求证
的定义域;(2) 求证 在
在 上是减函数;(3) 求函数
上是减函数;(3) 求函数 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com