【题目】椭圆
：
的左，右焦应分别是
，
，离心率为
，过且垂直于
轴的直线被椭圆截得的线段长为1.
（1）求椭圆的方程；
（2）已知直线
：
与椭圆切于点
，直线
平行于
，与椭圆交于不同的两点
、
，且与直线交于点
.证明：存在常数
，使得
，并求的值；
（3）点
是椭圆上除长轴端点外的任一点，连接
，
，设
后的角平分线
交的长轴于点
，求
的取值范围.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】某公司制定了一个激励销售人员的奖励方案:对于每位销售人员,均以10万元为基数,若销售利润没超出这个基数,则可获得销售利润的5%的奖金;若销售利润超出这个基数(超出的部分是a万元),则可获得
万元的奖金.记某位销售人员获得的奖金为y(单位:万元),其销售利润为x(单位:万元).
(1)写出这位销售人员获得的奖金y与其销售利润x之间的函数关系式;
(2)如果这位销售人员获得了
万元的奖金,那么他的销售利润是多少万元?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校高二年级的第二学期，因某学科的任课教师王老师调动工作，于是更换了另一名教师赵老师继任.第二学期结束后从全学年的该门课的学生考试成绩中用随机抽样的方法抽取了容量为50的样本，用茎叶图表示如下：
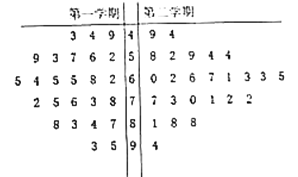
学校秉持均衡发展、素质教育的办学理念，对教师的教学成绩实行绩效考核，绩效考核方案规定：每个学期的学生成绩中与其中位数相差在
范围内（含）的为合格，此时相应的给教师赋分为1分；与中位数之差大于10的为优秀，此时相应的给教师赋分为2分；与中位数之差小于-10的为不合格，此时相应的给教师赋分为-1分.
（Ⅰ）问王老师和赵老师的教学绩效考核成绩的期望值哪个大？
（Ⅱ）是否有
的把握认为“学生成绩取得优秀与更换老师有关”.
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】等比数列{an}的各项均为正数，且2a1＋3a2＝1， 
＝9a2a6.
(1)求数列{an}的通项公式；
(2)设bn＝log3a1＋log3a2＋…＋log3an，求数列
的前n项和．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，把函数
的图象向右平移
个单位，再把图象上各点的横坐标缩小到原来的一半，纵坐标不变，得到函数
的图象，当
时，方程
恰有两个不同的实根，则实数
的取值范围为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的几何体中，四边形
是菱形，
是矩形，
，
，
， 
，
为
的中点.
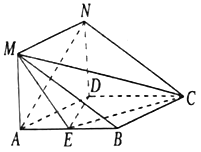
（1）平面
平面
（2）在线段
上是否存在点
，使二面角
的大小为
？若存在，求出
的长度；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设椭圆
的中心在坐标原点
，其中一个焦点为圆
的圆心，右顶点是圆
与
轴的一个交点.已知椭圆与直线
相交于
、
两点，延长
与椭圆交于点
.
（1）求椭圆的方程；
（2）求
面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一年之计在于春，一日之计在于晨，春天是播种的季节，是希望的开端.某种植户对一块地的
个坑进行播种，每个坑播3粒种子，每粒种子发芽的概率均为
，且每粒种子是否发芽相互独立.对每一个坑而言，如果至少有两粒种子发芽，则不需要进行补播种，否则要补播种.
（1）当
取何值时，有3个坑要补播种的概率最大？最大概率为多少？
（2）当
时，用
表示要补播种的坑的个数，求的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
