
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.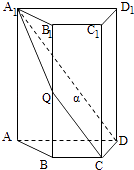
(1)证明:Q为BB1的中点;
(2)若AA1=4,CD=2,梯形ABCD的面积为6,∠ADC=60°,求平面α与底面ABCD所成锐二面角的大小.
【答案】
(1)证明:Ⅰ∵BQ∥AA1,BC∥AD,
BC∩BQ=B,AD∩AA1=A,
∴平面QBC∥平面A1AD,
∴平面A1CD与这两个平面的交线相互平行,
即QC∥A1D.
∴△QBC与△A1AD的对应边相互平行,
∴△QBC∽△A1AD,
∴ ![]() ,
,
∴Q为BB1的中点.
(2)解法一:如图1所示,在△ADC中,作AE⊥DC,垂足为E,连接A1E.
又DE⊥AA1,且AA1∩AE=A,
所以DE⊥平面AEA1,所以DE⊥A1E.
所以∠AEA1为平面α与底面ABCD所成二面角的平面角.
因为BC∥AD,AD=2BC,所以S△ADC=2S△BCA.
又因为梯形ABCD的面积为6,DC=2,
所以S△ADC=4,AE=4.
于是tan∠AEA1= ![]() =1,∠AEA1=
=1,∠AEA1= ![]() .
.
故平面α与底面ABCD所成二面角的大小为 ![]() .
.
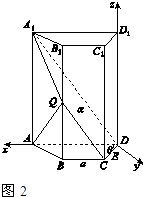
解法二:如图2所示,
以D为原点,DA,DD1分别为x轴和z轴正方向建立空间直角坐标系.
设∠CDA=θ,BC=a,则AD=2a.
因为S四边形ABCD= ![]() 2sin60°=6,
2sin60°=6,
所以a= ![]() .
.
从而可得C(1, ![]() ,0),A1(
,0),A1( ![]() ,0,4),
,0,4),
所以DC=(1, ![]() ,0),
,0), ![]() =(
=( ![]() ,0,4).
,0,4).
设平面A1DC的法向量 ![]() =(x,y,1),
=(x,y,1),
由 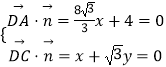 ,
,
得 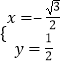 ,
,
所以 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,1).
,1).
又因为平面ABCD的法向量 ![]() =(0,0,1),
=(0,0,1),
所以cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
故平面α与底面ABCD所成二面角的大小为 ![]() .
.

【解析】(1)由已知得平面QBC∥平面A1AD,从而QC∥A1D,由此能证明Q为BB1的中点.(2)法一:在△ADC中,作AE⊥DC,垂足为E,连接A1E,∠AEA1为平面α与底面ABCD所成二面角的平面角,由此求出平面α与底面ABCD所成二面角的大小.(3)法二:以D为原点,DA,DD1分别为x轴和z轴正方向建立空间直角坐标系,由此利用向量法能求出平面α与底面ABCD所成二面角的大小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,E是棱DD1的中点.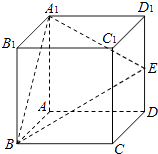
(1)求直线BE与平面ABB1A1所成的角的正弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,经过左焦点F1(-1,0)的直线l与椭圆G相交于A,B两点,与y轴相交于点C,且点C在线段AB上.
,经过左焦点F1(-1,0)的直线l与椭圆G相交于A,B两点,与y轴相交于点C,且点C在线段AB上.
(1)求椭圆G的方程;
(2)若|AF1|=|CB|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+be﹣x , (b∈R),函数g(x)=2asinx,(a∈R).
(1)求函数f(x)的单调区间;
(2)若b=﹣1,f(x)>g(x),x∈(0,π),求a取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知圆C的圆心C( ![]() ,
, ![]() ),半径r=
),半径r= ![]() .
.
(1)求圆C的极坐标方程;
(2)若α∈[0, ![]() ),直线l的参数方程为
),直线l的参数方程为 ![]() (t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
(t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:
(1)若从甲、乙两名学生中选择1人参加该知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2)若从学生甲的6次培训成绩中随机选择2个,记选到的分数超过87分的个数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2-6x+5≤0,q:x2-2x+1-m2≤0(m>0).
(1)若m=2,且p∧q为真,求实数x的取值范围;
(2)若p是q的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线 ![]() =1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
=1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com