
【题目】已知函数f(x)=2sinxcosx+2cos(x+ ![]() )cos(x﹣
)cos(x﹣ ![]() ).
).
(1)求f(x)的单调递减区间;
(2)设α∈(0,π),f( ![]() )=
)= ![]() ,求sinα的值.
,求sinα的值.
【答案】
(1)解:f(x)=sin2x+cos2x= ![]() sin(2x+
sin(2x+ ![]() ),
),
令2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
解得:kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
则f(x)的单调递减区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
(2)解:f( ![]() )=
)= ![]() sin(α+
sin(α+ ![]() )=
)= ![]() ,
,
∴α= ![]() ﹣
﹣ ![]() ,
,
则sinα=sin( ![]() ﹣
﹣ ![]() )=
)= ![]()
【解析】函数解析式第一项利用二倍角的正弦函数公式化简,第二项利用积化和差公式化简,整理后利用两角和与差的正弦函数公式化为一个角的正弦函数,(1)根据正弦函数的递减区间即可求出f(x)的递减区间;(2)由f( ![]() )=
)= ![]() ,求出α的度数,即可求出sinα的值.
,求出α的度数,即可求出sinα的值.
【考点精析】通过灵活运用两角和与差的正弦公式和正弦函数的单调性,掌握两角和与差的正弦公式:![]() ;正弦函数的单调性:在
;正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数即可以解答此题.
上是减函数即可以解答此题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】某校高三文科500名学生参加了5月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机数表法从中抽取100名学生的成绩进行统计分析,抽出的100名学生的数学、语文成绩如下表:

(1)将学生编号为:001,002,003,……,499,500.若从第5行第5列的数开始右读,请你依次写出最先抽出的5个人的编号(下面是摘自随机数表的第4行至第7行)

(2)若数学的优秀率为![]() ,求
,求![]() 的值;
的值;
(3)在语文成绩为良好的学生中,已知![]() ,求数学成绩“优”比“良”的人数少的概率.
,求数学成绩“优”比“良”的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是等差数列,前n项和为Sn , {bn}是单调递增的等比数列,b1=2是a1与a2的等差中项,a3=5,b3=a4+1,若当n≥m时,Sn≤bn恒成立,则m的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对边分别为a,b,c,已知 ![]() . (Ⅰ)若b=
. (Ⅰ)若b= ![]() ,当△ABC周长取最大值时,求△ABC的面积;
,当△ABC周长取最大值时,求△ABC的面积;
(Ⅱ)设 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=cos(2x+1)的图象,只要将函数y=cos2x的图象( )
A.向左平移1个单位
B.向右平移1个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届湖南省长沙市高三上学期统一模拟考试文数】已知过![]() 的动圆恒与
的动圆恒与![]() 轴相切,设切点为
轴相切,设切点为![]() 是该圆的直径.
是该圆的直径.
(Ⅰ)求![]() 点轨迹
点轨迹![]() 的方程;
的方程;
(Ⅱ)当![]() 不在y轴上时,设直线
不在y轴上时,设直线![]() 与曲线
与曲线![]() 交于另一点
交于另一点![]() ,该曲线在
,该曲线在![]() 处的切线与直线
处的切线与直线![]() 交于
交于![]() 点.求证:
点.求证: ![]() 恒为直角三角形.
恒为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间. 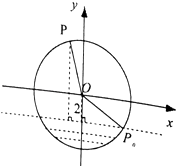
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com