
某蔬菜基地种植番茄,由历年市场行情得知,从二月一日起的300天内,番茄市场售价与上市时间的关系用图(1)的一条折线表示;番茄的种植成本与上市时间的关系用图(2)的抛物线表示.
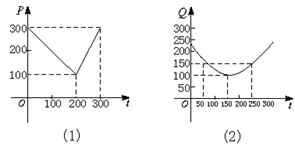
(1)写出图1表示的市场售价与时间的函数关系式P=f(t);图2表示的种植成本与时间的函数关系式Q=g(t);
(2)市场售价减去种植成本为纯收益,问何时上市的番茄纯收益最大?(注:市场售价和种植成本的单位:元/102 ,kg,时间单位:天)
(1)f(t)=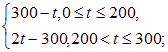 g(t)=
g(t)=![]() (t-150)2+100,0≤t≤300.
(t-150)2+100,0≤t≤300.
(2)从二月一日开始的第50天时,上市的番茄纯收益最大.
⑴由图1可得市场售价与时间的函数关系为:
f(t)=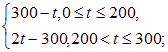
由图2可得种植成本与时间的函数关系为:
g(t)=![]() (t-150)2+100,0≤t≤300.
(t-150)2+100,0≤t≤300.![]()
![]()
⑵设t时刻的纯收益为h(t),由题意得h(t)=f(t)-g(t),
即h(t)=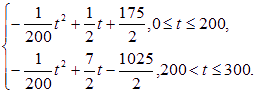
当0≤t≤200时,整理得h(t)=-![]() (t-50)2+100,
(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,整理得,h(t)=-![]() (t-350)2+100,
(t-350)2+100,
所以,当t=300时,h(t)取得区间(200,300)上的最大值87.5.
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的番茄纯收益最大.


 发散思维新课堂系列答案
发散思维新课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com