
���� ��1������x=��cos�ȣ�y=��sin�����ֱ�ߵ�ֱ�����귽�̣��Ӷ����AB�ij�����2����P����ֱ��l�����PM�ij����ɣ�
��� �⣺��1��������C�ļ����귽��Ϊ��2cos2��=1��
���2��cos2��-sin2�ȣ�=1��
��x2-y2=1��
��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$��tΪ��������
����x2-y2=1��
�ã�t2-2t-4=0��
��A��B��Ӧ�IJ����ֱ���t1��t2��
��t1+t2=2��t1t2=-4��
��|AB|=|t1-t2|=$\sqrt{{{��t}_{1}{+t}_{2}��}^{2}-{{4t}_{1}t}_{2}}$=2$\sqrt{5}$��
��2��P��ļ�����Ϊ��1��$\frac{��}{2}$����ֱ�������ǣ�0��1����
P��0��1����ֱ��l�ϣ�AB���е�M��Ӧ�IJ���Ϊ��
$\frac{{{t}_{1}+t}_{2}}{2}$=1����|PM|=1��
���� ���⿼����ֱ�߷����Լ��Լ������귽�̣�����㵽ֱ�ߵľ��빫ʽ����һ���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
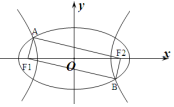 ��ͼF1��F2����ԲC1��$\frac{{x}^{2}}{4}$+y2=1��˫����C2�Ĺ������㣬A��B�ֱ���C1��C2�ڵڶ��������Ĺ����㣬���ı���AF1BF2Ϊ���Σ���C2���������ǣ�������
��ͼF1��F2����ԲC1��$\frac{{x}^{2}}{4}$+y2=1��˫����C2�Ĺ������㣬A��B�ֱ���C1��C2�ڵڶ��������Ĺ����㣬���ı���AF1BF2Ϊ���Σ���C2���������ǣ�������| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | $\frac{\sqrt{6}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��0�� | B�� | ��0��1�� | C�� | ��-2��-1�� | D�� | ��1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 1 | C�� | -1 | D�� | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
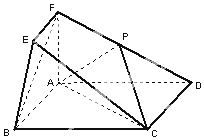 ����ͼ��ʾ�ļ������У��ı���ABCDΪ���Σ�ƽ��ABEF��ƽ��ABCD��EF��AB����BAF=90�㣬AD=2��AB=AF=2EF=l����P����DF�ϣ�
����ͼ��ʾ�ļ������У��ı���ABCDΪ���Σ�ƽ��ABEF��ƽ��ABCD��EF��AB����BAF=90�㣬AD=2��AB=AF=2EF=l����P����DF�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com