
【题目】在直角坐标系![]() 中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数,曲线
为参数,曲线![]() 上的点
上的点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)过O作线段![]() 的垂线,垂足为H,求点H的轨迹
的垂线,垂足为H,求点H的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 两点间的距离的取值范围.
两点间的距离的取值范围.
【答案】(1)![]() ;(2)
;(2)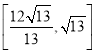
【解析】
(1)先将线![]() 的参数方程化为直角坐标方程,
的参数方程化为直角坐标方程,![]() 的极坐标化为直角坐标,代入曲线方程,化简得
的极坐标化为直角坐标,代入曲线方程,化简得![]() ,再根据三角形
,再根据三角形![]() 中等面积法,得到
中等面积法,得到![]() ,从而得H的轨迹是圆,得到点H的轨迹
,从而得H的轨迹是圆,得到点H的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)表示出![]() 两点间的距离
两点间的距离![]() ,再设
,再设![]() ,利用关系式
,利用关系式![]() ,将
,将![]() 也用
也用![]() 表示出来,则可得
表示出来,则可得![]() ,
,![]() ,再构造函数,利用导数研究函数的性质,求出
,再构造函数,利用导数研究函数的性质,求出![]() 两点间的距离的取值范围.
两点间的距离的取值范围.
(1)因为曲线![]() 的参数方程为
的参数方程为![]() 所以曲线
所以曲线![]() 的普通方程为
的普通方程为![]() .
.
因为曲线![]() 上的点
上的点![]() 的极坐标分别为
的极坐标分别为![]() ,
,
所以点![]() 的直角坐标分别为
的直角坐标分别为
![]() ,
,
代入曲线![]() 的方程得
的方程得![]() ,
,
所以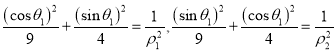 ,
,
所以两个式子相加得![]() .
.
由题意可知![]() ,所以
,所以![]() ,
,
所以点H的轨迹是圆, 所以点H的轨迹![]() 的方程为
的方程为![]() .
.
(2)![]() 两点间的距离为
两点间的距离为![]() ,设
,设![]() ,则
,则![]() ,
,
令函数![]() ,
,
所以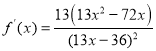 ,所以
,所以![]() 在区间
在区间![]() 上是减函数,
上是减函数,
在区间![]() 上是增函数. 又
上是增函数. 又![]() ,
,
所以函数![]() 的最大值为13,最小值为
的最大值为13,最小值为![]() ,
,
所以![]() 两点间的距离
两点间的距离![]() 的取值范围是
的取值范围是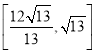 .
.


科目:高中数学 来源: 题型:
【题目】某手机生产企业为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到单价![]() (单位:千元)与销量
(单位:千元)与销量![]() (单位:百件)的关系如下表所示:
(单位:百件)的关系如下表所示:
单价 | 1 | 1.5 | 2 | 2.5 | 3 |
销量 | 10 | 8 | 7 | 6 |
|
已知![]() .
.
(Ⅰ)若变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(Ⅱ)用(Ⅰ)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() ,当销售数据
,当销售数据![]() 对应的残差满足
对应的残差满足![]() 时,则称
时,则称![]() 为一个“好数据”,现从5个销售数据中任取3个,求其中“好数据”的个数
为一个“好数据”,现从5个销售数据中任取3个,求其中“好数据”的个数![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: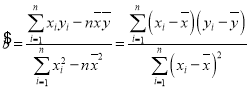 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某高中女学生中选取10名学生,根据其身高![]() 、体重
、体重![]() 数据,得到体重关于身高的回归方程
数据,得到体重关于身高的回归方程![]() ,用来刻画回归效果的相关指数
,用来刻画回归效果的相关指数![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A.这些女学生的体重和身高具有非线性相关关系
B.这些女学生的体重差异有60%是由身高引起的
C.身高为![]() 的女学生的体重一定为
的女学生的体重一定为![]()
D.这些女学生的身高每增加![]() ,其体重约增加
,其体重约增加![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线L的参数方程为:![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)求曲线C的参数方程;
(Ⅱ)当![]() 时,求直线l与曲线C交点的极坐标.
时,求直线l与曲线C交点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() 中底面边长、侧棱长都是4,
中底面边长、侧棱长都是4,![]() 别是
别是![]() 的中点,则以下四个结论中正确的是( )
的中点,则以下四个结论中正确的是( )
①![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;②
;②![]() 平行于平面
平行于平面![]() ;③三棱锥
;③三棱锥![]() 的体积为
的体积为![]() ;④
;④![]() 垂直于
垂直于![]() .
.
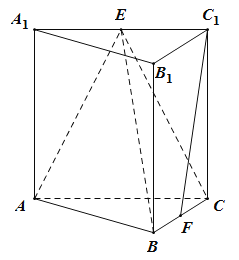
A.①②③B.②③④C.①③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直四棱柱![]() 的棱长均相等,且BAD=60,M是侧棱DD1的中点,N是棱C1D1上的点.
的棱长均相等,且BAD=60,M是侧棱DD1的中点,N是棱C1D1上的点.
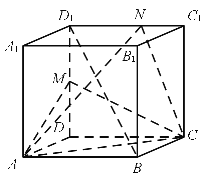
(1)求异面直线BD1和AM所成角的余弦值;
(2)若二面角![]() 的大小为
的大小为![]() ,,试确定点N的位置.
,,试确定点N的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示校情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续![]() 天每天新增感染人数不超过
天每天新增感染人数不超过![]() 人”,根据连续
人”,根据连续![]() 天的新增病例数计算,下列各项选项中,一定符合上述指标的是( )
天的新增病例数计算,下列各项选项中,一定符合上述指标的是( )
①平均数![]() ;
;
②标准差![]() ;
;
③平均数![]() ;且标准差
;且标准差![]() ;
;
④平均数![]() ;且极差小于或等于
;且极差小于或等于![]() ;
;
⑤众数等于![]() 且极差小于或等于
且极差小于或等于![]() .
.
A.①②B.③④C.③④⑤D.④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人![]() 次数学考试的成绩,统计结果如下表:
次数学考试的成绩,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若答对,则可参加复赛,否则被淘汰.
道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若至少答对其中
道,若至少答对其中![]() 道,则可参加复赛,否则被润汰.
道,则可参加复赛,否则被润汰.
已知学生甲、乙都只会![]() 道备选题中的
道备选题中的![]() 道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一条线段,且
上的一条线段,且![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的动点,则
上的动点,则
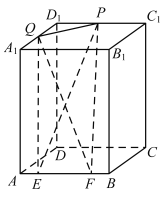
①四面体![]() 的体积为定值
的体积为定值
②直线![]() 到平面
到平面![]() 的距离为定值
的距离为定值
③点![]() 到直线
到直线![]() 的距离为定值
的距离为定值
④直线![]() 与平面
与平面![]() 所成的角为定值
所成的角为定值
其中正确结论的编号是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com