
| 4 |
| - |
| 9 |
| - |
| 4 |
| a |
| 9 |
| b |
| 4 |
| a |
| 9 |
| b |
| 4b |
| a |
| 9a |
| b |
| 4 |
| a |
| 9 |
| b |
| 4 |
| a |
| 9 |
| b |
| 4b |
| a |
| 9a |
| b |
|
| 4b |
| a |
| 9a |
| b |
| 3 |
| 2 |
| 4 |
| a |
| 9 |
| b |


科目:高中数学 来源: 题型:
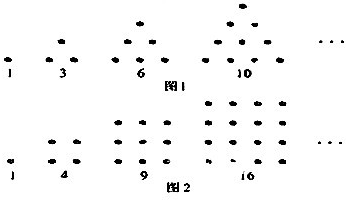
| A、289 | B、1024 | C、1225 | D、1378 |
查看答案和解析>>
科目:高中数学 来源: 题型:
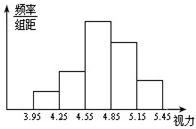 中小学生的视力状况受到全社会的广泛关注,某市有关部门对全市3万名高中生的视力状况进行一次抽样调查统计,所得到的有关数据绘制成频率分布直方图,如图,从左至右五个小组的频率之比依次是2:4:9:7:3,第五小组的频数是36.
中小学生的视力状况受到全社会的广泛关注,某市有关部门对全市3万名高中生的视力状况进行一次抽样调查统计,所得到的有关数据绘制成频率分布直方图,如图,从左至右五个小组的频率之比依次是2:4:9:7:3,第五小组的频数是36.查看答案和解析>>
科目:高中数学 来源: 题型:
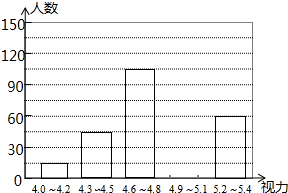 为进一步加强中小学生近视眼的防控工作,市教育局近期下发了有关文件,将学生视力保护工作纳入学校和教师的考核内容,为此,某县教育组管部门对今年初中毕业生的视力进行了一次抽样调查,并根据调查结果绘制如下频数分布表和频数分布直方图的一部分.
为进一步加强中小学生近视眼的防控工作,市教育局近期下发了有关文件,将学生视力保护工作纳入学校和教师的考核内容,为此,某县教育组管部门对今年初中毕业生的视力进行了一次抽样调查,并根据调查结果绘制如下频数分布表和频数分布直方图的一部分.| 视力 | 频数(人) | 频率 |
| 4.0~4.2 | 15 | 0.05 |
| 4.3~4.5 | 45 | 0.15 |
| 4.6~4.8 | 105 | 0.35 |
| 4.9~5.1 | a | 0.25 |
| 5.2~5.4 | 60 | b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com