练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，其中．

    （I）若，求在区间上的最大值和最小值；

    （II）解关于x的不等式

    【答案】（1）最小值为，最大值为；（2）见解析

    【解析】试题分析：（Ⅰ）a=1时，f（x）=（x﹣2）x=（x﹣1）2﹣1，由此能求出f（x）在区间[0，3]上的最大值和最小值，（Ⅱ）当a＞0时，原不等式同解于（x﹣2）（x﹣）＞0，当a＜0时，原不等式同解于（x﹣2）（x﹣）＜0，由此能求出当a＞0时，不等式的解集为{x|x＞2或x＜}；当﹣1＜a＜0时，不等式的解集为{x|2＜x＜}；当a=﹣1时，不等式的解集为；当a＜﹣1时，不等式的解集为．

    详解：

    (Ⅰ)最小值为，最大值为；

    (Ⅱ)当时，不等式解集为

    当时，不等式解集为

    当时，不等式解集为

    当时，不等式解集为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某初级中学有三个年级，各年级男、女人数如下表：

    初一年级

    初二年级

    初三年级

    女生

    370

    200

    男生

    380

    370

    300

    已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.
    （1）求 的值；
    （2）用分层抽样的方法在初三年级中抽取一个容量为5的样本，求该样本中女生的人数；
    （3）用随机抽样的方法从初二年级女生中选出8人，测量它们的左眼视力，结果如下：1.2，1.5，1.2，1.5，1.5，1.3，1.0，1.2．把这8人的左眼视力看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0.1的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆 ： （其中 为圆心）上的每一点横坐标不变，纵坐标变为原来的一半，得到曲线 .
    （1）求曲线 的方程；
    （2）若点 为曲线 上一点，过点 作曲线 的切线交圆 于不同的两点 （其中 在 的右侧），已知点 .求四边形 面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.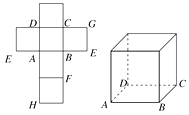

    （1）请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由)；
    （2）判断平面BEG与平面ACH的位置关系．并说明你的结论；
    （3）证明：直线DF⊥平面BEG.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的右焦点为 ，上顶点为 ， 周长为 ，离心率为 .
    （1）求椭圆 的方程；
    （2）若点 是椭圆 上第一象限内的一个点，直线 过点 且与直线 平行，直线 且 与椭圆 交于 两点，与 交于点 ，是否存在常数 ，使 .若存在，求出 的值，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆 （ ）的右焦点为F，右顶点为A，已知 ，其中O 为原点， e为椭圆的离心率.
    （Ⅰ）求椭圆的方程；
    （Ⅱ）设过点A的直线l与椭圆交于点B（B不在x轴上），垂直于l的直线与l交于点M，与y轴交于点H，若 ，且 ，求直线的l斜率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足，且，其前n项之和为Sn，则满足不等式的最小自然数n是 ___.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从装有 2个红球和 2个白球的口袋中任取 2个球，则下列每对事件中，互斥事件的对数是( )对

    （1）“至少有 1个白球”与“都是白球” （2）“至少有 1个白球”与“至少有 1个红球”

    （3）“至少有 1个白球”与“恰有 2个白球” （4）“至少有 1个白球”与“都是红球”

    A. 0 B. 1 C. 2 D. 3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，三棱锥P﹣ABC中，△ABC是边长为3的等边三角形，D是线段AB的中点，DE∩PB=E，且DE⊥AB，若∠EDC=120°，PA= ，PB= ，则三棱锥P﹣ABC的外接球的表面积为 ．

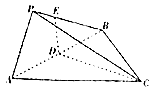
    查看答案和解析>>

    同步练习册答案