练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．设x，y满足$\left\{\begin{array}{l}2x+y≥4\\ x-y≥1\\ x-2y≤2\end{array}\right.$，则z=x+y的最小值为2．

    分析 作出不等式组表示的可行域，作出直线y=-x，由z的几何意义：直线在y轴上截距．平移直线y=-x，观察即可得到所求最小值．

    解答 解：作出不等式组表示的可行域，如右图．
    作出直线y=-x，
    z=x+y的几何意义是直线在y轴上的截距．
    平移直线y=-x，
    由y=4-2x代入直线x-2y-2=0，可得x=2，y=0．
    将A（2，0）代入z=x+y，
    可得z的最小值为2．
    故答案为：2．

    点评 本题考查简单线性规划的运用，注意作出可行域，运用平移法，考查运算能力和数形结合思想，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．如图（1），在等腰梯形ABCD中，AB∥CD，E，F分别为AB和CD的中点，且AB=EF=2，CD=6，M为BC中点，现将梯形BEFC沿EF所在直线折起，使平面EFCB⊥平面EFDA，如图（2）所示，N是线段CD上一动点，且CN=λND．
    （Ⅰ）当$λ=\frac{1}{2}$时，求证：MN∥平面ADFE；
    （Ⅱ）当λ=1时，求二面角M-NA-F的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知M1={第一象限角}，M2={锐角}．M3={0°～90°的角}，M4={小于90°的角}，则（　　）
    A．M1=M2=M3=M4B．M1?M2?M3?M4C．M1⊆M2⊆M3⊆M4D．M2⊆M3且M2⊆M4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．某班50名学生中有女生20名，按男女比例用分层抽样的方法，从全班学生中抽取部分学生进行调查，已知抽到的女生有4名，则本次调查抽取的人数是（　　）
    A．8B．10C．12D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

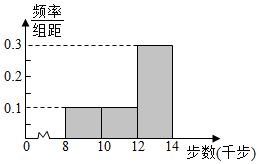    11．王师傅为响应国家开展全民健身运动的号召，每天坚持“健步走”，并用计步器对每天的“健步走”步数进行统计，他从某个月中随机抽取10天“健步走”的步数，绘制出的频率分布直方图如图所示．
    （1）试估计该月王师傅每天“健步走”的步数的中位数及平均数（精确到小数点后1位）；
    （2）某健康组织对“健步走”结果的评价标准为：
    每天的步数分组
    （千步）    		[8，10）[10，12）[12，14]
    评价级别及格良好优秀
    现从这10天中评价级别是“良好”或“及格”的天数里随机抽取2天，求这2天的“健步走”结果属于同一评价级别的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．甲、乙、丙、丁和戊5名学生进行劳动技术比赛，决出第一名到第五名的名次．甲乙两名参赛者去询问成绩，回答者对甲说“很遗憾，你没有得到冠军”；对乙说“你当然不会是最差的”，从上述回答分析，5人的名次排列可能有78种不同情况．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．（1）若点P（2，-1）为圆（x-1）2+y2=25的弦AB的中点，求直线AB的方程．
    （2）若直线y=2x+b与圆x2+y2=4相交A，B两点，求弦AB中点M的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．如图，将正整数排成一个三角形数阵：

    按照以上排列的规律，第20行从左向右的第2个数为192．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．观察下列算式：
    13=1
    23=3+5
    33=7+9+11
    43=13+15+17+19
    …
    若某数m3按上述规律展开后，发现等式右边含有”2661“这个数，则m=52．

    查看答案和解析>>

    同步练习册答案