Question

设集合S={1，2，3，4，5，6}，定义集合组（A，B）：A⊆S，B⊆S，A中含有3个元素，B中至少含有2个元素，且集合B中最小的元素不小于A中最大的元素．若满足AUB=S，则称这样的集合组（A，B）为“完美集合组”．在所有集合组（A，B）中任取一组，则恰好取得“完美集合组”的率为（ ）
A．
B．
C．
D．

Answer 1

【答案】分析：根据集合A中只含有3个元素，则可对集合A进行分类讨论，逐一求出集合B的所以情况即可．
解答：解：当集合A={1，2，3}时，则B={3，4，5，6}、{3，4，5}、{3，4，6}、{4，5，6}、{3，5，6}、
{3，4}、{3，5}、{3，6}、{4，5}、{4，6}、{5，6}，共有11个．
当集合A={1，2，4}时，则B={4，5，6}、{4，5}、{4，6}、{5，6}，共有4个．
当集合A={1，3，4}时，集合B={4，5，6}、{4，5}、{4，6}、{5，6}，共有4个．
当集合A={2，3，4}时，集合B={4，5，6}、{4，5}、{4，6}、{5，6}，共有4个．
当集合A={1，2，5}时，集合B={5，6}，共有1个．
当集合A={1，3，5}时，集合B={5，6}，共有1个．
当集合A={1，4，5}时，集合B={5，6}，共有1个．
当集合A={2，3，5}时，集合B={5，6}，共有1个．
当集合A={2，4，5}时，集合B={5，6}，共有1个．
当集合A={3，4，5}时，集合B={5，6}，共有1个．
综上，所有的集合组（A，B），共有29个，其中，满足（A，B）为“完美集合组”的有：
①A={1，2，3}、B={4，5，6}； ②A={1，2，3}、B={3，4，5，6}，共有2组，
故所有集合组（A，B）中任取一组，则恰好取得“完美集合组”的概率等于，
故选D．
点评：本题主要考查了集合子集的运算，分类讨论的数学思想，属于基础题．
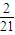
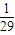