
【题目】给出下列命题:
①在△ABC中,若A<B,则sinA<sinB;
②在同一坐标系中,函数y=sinx与y=lgx的交点个数为2个;
③函数y=|tan2x|的最小正周期为 ![]() ;
;
④存在实数x,使2sin(2x﹣ ![]() )﹣1=
)﹣1= ![]() 成立;
成立;
其中正确的命题为(写出所有正确命题的序号).
【答案】①③
【解析】解:①在△ABC中,若A<B,由正弦定理得a<b,则由 ![]() 得sinA<sinB成立,故①正确;
得sinA<sinB成立,故①正确;
②在同一坐标系中,作出函数y=sinx与y=lgx图象如图:
∵lg10=1,∴两个图象的交点个数为3个;故②错误,
③函数y=|tan2x|的最小正周期和y=tan2x的周期相同,为T= ![]() ,故③正确,;
,故③正确,;
④由2sin(2x﹣ ![]() )﹣1=
)﹣1= ![]() ,得sin(2x﹣
,得sin(2x﹣ ![]() )=
)= ![]() >1,
>1,
则不存在实数x,使2sin(2x﹣ ![]() )﹣1=
)﹣1= ![]() 成立;故④错误,
成立;故④错误,
所以答案是:①③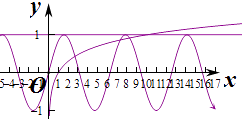
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin(2x+
sin(2x+ ![]() ),其中x∈R,下列结论中正确的是( )
),其中x∈R,下列结论中正确的是( )
A.f(x)是最小正周期为π的偶函数
B.f(x)的一条对称轴是 ![]()
C.f(x)的最大值为2
D.将函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位得到函数f(x)的图象
个单位得到函数f(x)的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共l2分)
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D.
(Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值;
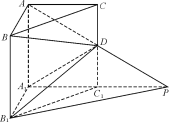
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)=Asin(ωx+)(A>0,ω>0,||< ![]() )的部分图象如图所示:
)的部分图象如图所示: 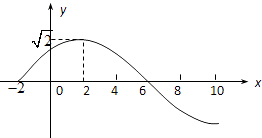
(1)求函数f(x)的解析式;
(2)若g(x)的图象是将f(x)的图象先向右平移1个单位,然后纵坐标不变横坐标缩短到原来的一半得到的,求g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100] 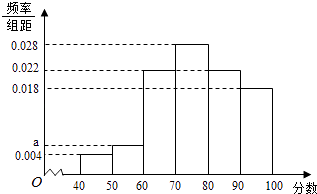
(1)求频率分布图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次![]() 公里的自行车个人赛中,25名参赛选手的成绩(单位:分钟)的茎叶图如图所示:
公里的自行车个人赛中,25名参赛选手的成绩(单位:分钟)的茎叶图如图所示:

(1)现将参赛选手按成绩由好到差编为1~25号,再用系统抽样方法从中选取5人,已知选手甲的成绩为85分钟,若甲被选取,求被选取的其余4名选手的成绩的平均数;
(2)若从总体中选取一个样本,使得该样本的平均水平与总体相同,且样本的方差不大于7,则称选取的样本具有集中代表性,试从总体(25名参赛选手的成绩)选取一个具有集中代表性且样本容量为5的样本,并求该样本的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(Ⅰ)若直线l不经过第二象限,求实数a的取值范围;
(Ⅱ)若直线l与两坐标轴围成的三角形面积等于2,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com