
分析 P(ξ)是“ξ个人命中,3-ξ个人未命中”的概率.其中ξ的可能取值为0,1,2,3.则P(ξ=1)-P(ξ=0)≥0,P(ξ=1)-P(ξ=2)≥0,P(ξ=1)-P(ξ=3)≥0.及其0<a<1,解出即可得出.
解答 解:P(ξ)是“ξ个人命中,3-ξ个人未命中”的概率.其中ξ的可能取值为0,1,2,3.
P(ξ=0)=${C}_{1}^{0}•(1-\frac{1}{2})$•${∁}_{2}^{0}(1-a)^{2}$=$\frac{1}{2}(1-a)^{2}$,P(ξ=1)=${∁}_{1}^{1}•\frac{1}{2}{∁}_{2}^{0}(1-a)^{2}$+${∁}_{1}^{0}(1-\frac{1}{2})•{∁}_{2}^{1}a(1-a)$=$\frac{1}{2}(1-{a}^{2})$,
P(ξ=2)=${∁}_{1}^{1}•\frac{1}{2}•{∁}_{2}^{1}a(1-a)$+${∁}_{1}^{0}(1-\frac{1}{2}){∁}_{2}^{2}{a}^{2}$=$\frac{1}{2}(2a-{a}^{2})$,P(ξ=3)=${∁}_{1}^{1}•\frac{1}{2}•{∁}_{2}^{2}$a2=$\frac{1}{2}{a}^{2}$.
P(ξ=1)-P(ξ=0)=$\frac{1}{2}(1-{a}^{2})$-$\frac{1}{2}(1-a)^{2}$=a(1-a),
P(ξ=1)-P(ξ=2)=$\frac{1}{2}(1-{a}^{2})$-$\frac{1}{2}(2a-{a}^{2})$=$\frac{1-2a}{2}$,
P(ξ=1)-P(ξ=3)=$\frac{1}{2}(1-{a}^{2})$-$\frac{1}{2}{a}^{2}$=$\frac{1-2{a}^{2}}{2}$.
由a(1-a)≥0,$\frac{1-2a}{2}$≥0,$\frac{1-2{a}^{2}}{2}$≥0,0<a<1,得$0<a≤\frac{1}{2}$,即a的取值范围是$(0,\frac{1}{2}]$.
故答案为:$(0,\frac{1}{2}]$.
点评 本题考查了相互独立事件与互斥事件的概率计算公式及其性质、不等式的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
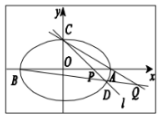 过点C(0,$\sqrt{2}$)的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆与x轴交于两点A(a,0),B(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与BD交于点Q.
过点C(0,$\sqrt{2}$)的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆与x轴交于两点A(a,0),B(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与BD交于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
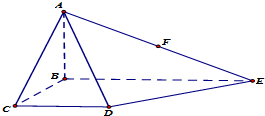 如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.
如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x0∈A,2x0∈B | B. | ¬p:?x0∉A,2x0∈B | C. | ¬p:?x0∈A,2x0∉B | D. | ¬p:?x∉A,2x∉B |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com