
【题目】设函数f(x)是定义在(﹣∞,+∞)上的增函数,实数a使得f(1﹣ax﹣x2)<f(2﹣a)对于任意x∈[0,1]都成立,则实数a的取值范围是( )
A.(﹣∞,1)
B.[﹣2,0]
C.(﹣2﹣2 ![]() ,﹣2+2
,﹣2+2 ![]() )
)
D.[0,1]
【答案】A
【解析】解:法一:由条件得1﹣ax﹣x2<2﹣a对于x∈[0,1]恒成立
令g(x)=x2+ax﹣a+1,只需g(x)在[0,1]上的最小值大于0即可.
g(x)=x2+ax﹣a+1=(x+ ![]() )2﹣
)2﹣ ![]() ﹣a+1.
﹣a+1.
①当﹣ ![]() <0,即a>0时,g(x)min=g(0)=1﹣a>0,∴a<1,故0<a<1;
<0,即a>0时,g(x)min=g(0)=1﹣a>0,∴a<1,故0<a<1;
②当0≤﹣ ![]() ≤1,即﹣2≤a≤0时,g(x)min=g(﹣
≤1,即﹣2≤a≤0时,g(x)min=g(﹣ ![]() )=﹣
)=﹣ ![]() ﹣a+1>0,∴﹣2﹣2
﹣a+1>0,∴﹣2﹣2 ![]() <a<﹣2+2
<a<﹣2+2 ![]() ,故﹣2≤a≤0;
,故﹣2≤a≤0;
③当﹣ ![]() >1,即a<﹣2时,g(x)min=g(1)=2>0,满足,故a<﹣2.
>1,即a<﹣2时,g(x)min=g(1)=2>0,满足,故a<﹣2.
综上a<1.
法二:由1﹣ax﹣x2<2﹣a得(1﹣x)a<x2+1,
∵x∈[0,1],∴1﹣x≥0,
∴①当x=1时,0<2恒成立,此时a∈R;
②当x∈[0,1)时,a< ![]() 恒成立.
恒成立.
求当x∈[0,1)时,函数y= ![]() 的最小值.
的最小值.
令t=1﹣x(t∈(0,1]),则y= ![]() =
= ![]() =t+
=t+ ![]() ﹣2,
﹣2,
而函数y=t+ ![]() ﹣2是(0,1]上的减函数,所以当且仅当t=1,即x=0时,ymin=1.
﹣2是(0,1]上的减函数,所以当且仅当t=1,即x=0时,ymin=1.
故要使不等式在[0,1)上恒成立,只需a<1,
由①②得a<1.
故选:A
解法一:由条件得1﹣ax﹣x2<2﹣a对于x∈[0,1]恒成立,令g(x)=x2+ax﹣a+1,只需g(x)在[0,1]上的最小值大于0即可,分类讨论,求最值即可求出实数a的取值范围;
解法二:由1﹣ax﹣x2<2﹣a,得(1﹣x)a<x2+1,对x讨论,再分离参数,求最值,即可求出实数a的取值范围.


科目:高中数学 来源: 题型:
【题目】有一块半径为 ![]() (
( ![]() 是正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池
是正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池 ![]() 和其附属设施,附属设施占地形状是等腰
和其附属设施,附属设施占地形状是等腰 ![]() ,其中
,其中 ![]() 为圆心,
为圆心, ![]() ,
, ![]() 在圆的直径上,
在圆的直径上, ![]() ,
, ![]() ,
, ![]() 在半圆周上,如图.设
在半圆周上,如图.设 ![]() ,征地面积为
,征地面积为 ![]() ,当
,当 ![]() 满足
满足 ![]() 取得最大值时,开发效果最佳,开发效果最佳的角
取得最大值时,开发效果最佳,开发效果最佳的角 ![]() 和
和 ![]() 的最大值分别为( )
的最大值分别为( )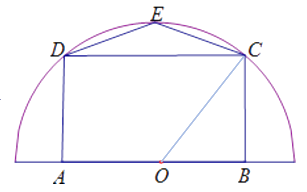
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设M=10a2+81a+207,P=a+2,Q=26﹣2a,若将lgM,lgQ,lgP适当排序后可构成公差为1的等差数列{an}的前三项. (Ⅰ)求a的值及{an}的通项公式;
(Ⅱ)记函数 ![]() 的图像在x轴上截得的线段长为bn , 设
的图像在x轴上截得的线段长为bn , 设 ![]() ,求Tn .
,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为1,前n项和Sn与an之间满足an= ![]() (n≥2,n∈N*)
(n≥2,n∈N*)
(1)求证:数列{ ![]() }是等差数列;
}是等差数列;
(2)求数列{an}的通项公式;
(3)设存在正整数k,使(1+S1)(1+S1)…(1+Sn)≥k ![]() 对于一切n∈N*都成立,求k的最大值.
对于一切n∈N*都成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(1,﹣2)和( ![]() ,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(0, ![]() )∪(
)∪( ![]() ,π)
,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为(2﹣m)x+(2m+1)y+3m+4=0,其中m∈R.
(1)求证:直线l恒过定点;
(2)当m变化时,求点P(3,1)到直线l的距离的最大值;
(3)若直线l分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为 . 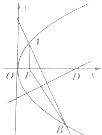
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an>0,n=1,2,…,且a5a2n﹣5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n﹣1=( )
A.n(2n﹣1)
B.(n+1)2
C.n2
D.(n﹣1)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com