
����Ŀ�������ĸ�����Բ���ߵ������У�
��˫���� ![]() ����Բ
����Բ ![]() ����ͬ�Ľ��㣻
����ͬ�Ľ��㣻
���������ߵĽ����ң��������ֱ�߽����������õ��߶Σ�Ϊֱ����Բ�������ߵ��������еģ�
����A��BΪ�������㣬kΪ��������|PA|��|PB|=k����P�Ĺ켣Ϊ˫���ߣ�
�ܹ���ԲC��һ��A��Բ�Ķ���AB��OΪԭ�㣬�� ![]() ��P�Ĺ켣Ϊ��Բ��������ȷ�ĸ����ǣ� ��
��P�Ĺ켣Ϊ��Բ��������ȷ�ĸ����ǣ� ��
A.1��
B.2��
C.3��
D.4��
���𰸡�B
���������⣺��˫���� ![]() �Ľ�������Ϊ����5��0����
�Ľ�������Ϊ����5��0����
��Բ ![]() �Ľ�������Ϊ����5��0����
�Ľ�������Ϊ����5��0����
����˫���� ![]() ����Բ
����Բ ![]() ����ͬ�Ľ��㣬��ȷ��
����ͬ�Ľ��㣬��ȷ��
�ڲ�����������Ϊ�������ߣ�y2=2px ��p��0 ������������λ��Y����Ҳ࣬��X��Ϊ�Գ��ᣮ
����������ΪPQ��PQ���е���M��M���ߵľ�����d��
��P���ߵľ���d1=|PF|��Q���ߵľ���d2=|QF|��
��M���ߵľ���d�����ε���λ�ߣ�����d= ![]() ��
��
�������ߵĶ���ɵã� ![]() =
= ![]() =�뾶��
=�뾶��
����Բ��M���ߵľ�����ڰ뾶��
����Բ���������У���ȷ��
��ƽ��������������F1��F2�ľ���IJ�ľ���ֵ���ڳ���k��k��|F1F2|���ĵ�Ĺ켣����˫���ߣ�
��0��k��|AB|ʱ��˫���ߵ�һ֧����k=|AB|ʱ����ʾ���ߣ����Բ���ȷ��
���趨ԲC�ķ���Ϊx2+y2+Dx+Ey+F=0����A��m��n����P��x��y����
�� ![]() ���֪PΪAB���е㣬��B��2x��m��2y��n����
���֪PΪAB���е㣬��B��2x��m��2y��n����
��ΪABΪԲ�Ķ��ң�����B����֪Բ�ϣ�
��B���������Բx2+y2+Dx+Ey+F=0�õ�P�Ĺ켣��ΪԲ��
��B��A�غ�ʱAB�����ң����Ե�A���⣬���Բ���ȷ��
���Դ��ǣ�B��


 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() Ϊ�ȱ���������
Ϊ�ȱ��������� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() Ϊ
Ϊ![]() ���е�.
���е�.
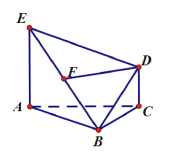
������֤�� ![]() ƽ��
ƽ��![]() ��
��
������֤��ƽ��![]() ƽ��
ƽ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ե�A����1��2��ΪԲ�ĵ�Բ��ֱ��m��x+2y+7=0���У�����B����2��0���Ķ�ֱ��l��ԲA�ཻ��M��N����
��1����ԲA�ķ��̣�
��2����|MN|=2 ![]() ʱ����ֱ��l���̣�
ʱ����ֱ��l���̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��x��2y+2m��2=0��
��1������㣨2��3������ֱ��l��ֱ��ֱ�ߵķ��̣�
��2����ֱ��l������������Χ�ɵ������ε��������4����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ��Ϊ
��Բ��Ϊ![]() ���뾶Ϊ1����
���뾶Ϊ1����![]() .
.
������д��Բ![]() �ı����������жϵ�
�ı����������жϵ�![]() ��Բ
��Բ![]() ��λ�ù�ϵ��
��λ�ù�ϵ��
��������һ�����ߴӵ�![]() �������
�������![]() �ᷴ�����������߾���Բ��
�ᷴ�����������߾���Բ��![]() ���������������ֱ�ߵķ���.
���������������ֱ�ߵķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=2px��p��0�����ϵĵ�M��1��m�����佹��F�ľ���Ϊ2��
������C�ķ��̣��������߷��̣�
��II����֪A ��1����2�����Ƿ����ƽ����OA��OΪ����ԭ�㣩��ֱ��L��ʹ��ֱ��L��������C�й����㣬��ֱ��OA��L�ľ������ ![]() �������ڣ���ֱ��L�ķ��̣��������ڣ�˵�����ɣ�
�������ڣ���ֱ��L�ķ��̣��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һֱ������Բ4x2+9y2=36�ཻ��A��B���㣬��AB���е�����ΪM��1��1������ֱ��AB����Ϊ�� ��
A.4x+9y��13=0
B.4x+9y+13=0
C.9x+4y��13=0
D.9x+4y+13=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��y=kx+1��k��0������Բ3x2+y2=a�ཻ��A��B������ͬ�ĵ㣬��l��y��Ľ���ΪC��
������k=1����|AB|= ![]() ����ʵ��a��ֵ��
����ʵ��a��ֵ��
������ ![]() =2
=2 ![]() �����AOB��������ֵ������ʱ��Բ�ķ��̣�
�����AOB��������ֵ������ʱ��Բ�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʺ�����������Բ���ߵı����̣�
��1����Բ����A��2�� ![]() ����B��
����B�� ![]() ��
�� ![]() ����
����
��2����˫����C1�� ![]() �й��������ߣ��ҽ���Ϊ8��˫����C2���̣�
�й��������ߣ��ҽ���Ϊ8��˫����C2���̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com