
定义:在数列 中,若
中,若 ,(n≥2,n∈N*,p为常数),则称
,(n≥2,n∈N*,p为常数),则称 为“等方差数列”.下列是对“等方差数列”的有关判断:
为“等方差数列”.下列是对“等方差数列”的有关判断:
①若 是“等方差数列”,则数列
是“等方差数列”,则数列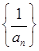 是等差数列;②
是等差数列;② 是“等方差数列”;
是“等方差数列”;
③若 是“等方差数列”,则数列
是“等方差数列”,则数列 (k∈N*,k为常数)也是“等方差数列”;
(k∈N*,k为常数)也是“等方差数列”;
④若 既是“等方差数列”,又是等差数列,则该数列是常数数列.
既是“等方差数列”,又是等差数列,则该数列是常数数列.
其中正确的命题为 .(写出所有正确命题的序号)
③④
【解析】因为①:可以举反例.如an=0时数列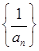 不存在,所以①错误
不存在,所以①错误
②:对数列{(-2)n}有an2-an-12=[(-2)n]2-[(-2)n-1]2=4n-4n-1不是常数,所以②错误
③:对数列{akn}有akn2-ak(n-1)2=(akn2-akn-12)+(akn-12-akn-22)+…+(akn-k+12-akn-k2)=kp,而k,p均为常数,所以数列{akn}也是“等方差数列”,所以③正确
④:设数列{an}首项a1,公差为d则有a2=a1+d,a3=a1+2d,所以有(a1+d)2-a12=p,且(a1+2d)2-(a1+d)2=p,所以得d2+2a1d=p,3d2+2a1d=p,上两式相减得d=0,所以此数列为常数数列,所以④正确.
故答案为:③④


科目:高中数学 来源:2010年浙江省宁波市八校联考高一第二学期期末数学试题 题型:填空题
定义:在数列 中,若
中,若 ,(n≥2,n∈N*,p为常数),则称
,(n≥2,n∈N*,p为常数),则称 为“等方差数列”.下列是对“等方差数列”的有关判断:
为“等方差数列”.下列是对“等方差数列”的有关判断:
①若 是“等方差数列”,则数列
是“等方差数列”,则数列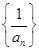 是等差数列;②
是等差数列;② 是“等方差数列”;
是“等方差数列”;
③若 是“等方差数列”,则数列
是“等方差数列”,则数列 (k∈N*,k为常数)也是“等方差数列”;
(k∈N*,k为常数)也是“等方差数列”;
④若 既是“等方差数列”,又是等差数列,则该数列是常数数列.
既是“等方差数列”,又是等差数列,则该数列是常数数列.
其中正确的命题为 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:2010-2011年湖北省高一期中考试数学理卷 题型:填空题
.定义:在数列 中,若
中,若 ,(
,(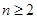 ,
,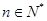 ,
,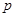 为常数),则称
为常数),则称 为“等方差数列”.下列是对“等方差数列”的有关判断:
为“等方差数列”.下列是对“等方差数列”的有关判断:
①若 是“等方差数列”,则数列
是“等方差数列”,则数列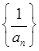 是等差数列;
是等差数列;
② 是“等方差数列”;
是“等方差数列”;
③若 是“等方差数列”,则数列
是“等方差数列”,则数列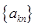 (
( ,
, 为常数)也是“等方差数列”;
为常数)也是“等方差数列”;
④若 既是“等方差数列”,又是等差数列,则该数列是常数数列.
既是“等方差数列”,又是等差数列,则该数列是常数数列.
其中正确的命题为 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:重庆市万州高级中学2010级高考适应性考试(理) 题型:填空题
定义:在数列 中,若
中,若 ,则称数列
,则称数列 为“等方差数列”。下列是对“等方差数列”的判断有:
为“等方差数列”。下列是对“等方差数列”的判断有:
①若 是等方差数列,则
是等方差数列,则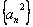 是等差数列;
是等差数列;
②数列 是等方差数列;
是等方差数列;
③若 是等方差数列,则数列
是等方差数列,则数列 也是等方差数列;
也是等方差数列;
④若 是等方差数列,又是等差数列,则该数列为常数列;
是等方差数列,又是等差数列,则该数列为常数列;
其中正确命题的序号为___________;
查看答案和解析>>
科目:高中数学 来源:2010-2011年湖北省黄冈中学高一期中考试数学理卷 题型:填空题
.定义:在数列 中,若
中,若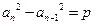 ,(
,( ,
, ,
, 为常数),则称
为常数),则称 为“等方差数列”.下列是对“等方差数列”的有关判断:
为“等方差数列”.下列是对“等方差数列”的有关判断:
①若 是“等方差数列”,则数列
是“等方差数列”,则数列 是等差数列;
是等差数列;
② 是“等方差数列”;
是“等方差数列”;
③若 是“等方差数列”,则数列
是“等方差数列”,则数列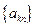 (
( ,
, 为常数)也是“等方差数列”;
为常数)也是“等方差数列”;
④若 既是“等方差数列”,又是等差数列,则该数列是常数数列.
既是“等方差数列”,又是等差数列,则该数列是常数数列.
其中正确的命题为 .(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com