
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC=![]()
![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD.

(1)证明:ED∥面PAB;
(2)若PC=2,PA=![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
【答案】(Ⅰ)证明过程如解析;(Ⅱ)![]()
【解析】试题分析:(Ⅰ)取PB的中点F,连接AF,EF,由三角形的中位线定理可得四边形ADEF是平行四边形.得到DE∥AF,再由线面平行的判定可得ED∥面PAB;(Ⅱ)法一、取BC的中点M,连接AM,由题意证得A在以BC为直径的圆上,可得AB⊥AC,找出二面角A-PC-D的平面角.求解三角形可得二面角A-PC-D的余弦值.
试题解析:(Ⅰ)证明:取PB的中点F,连接AF,EF.
∵EF是△PBC的中位线,∴EF∥BC,且EF=![]()
![]() .
.
又AD=BC,且AD=![]()
![]() ,∴AD∥EF且AD=EF,
,∴AD∥EF且AD=EF,
则四边形ADEF是平行四边形.
∴DE∥AF,又DE面ABP,AF面ABP,∴ED∥面PAB
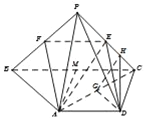
(Ⅱ)法一、取BC的中点M,连接AM,则AD∥MC且AD=MC,
∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上.∴AB⊥AC,可得![]()
![]() .
.
过D作DG⊥AC于G,
∵平面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,
∴DG⊥平面PAC,则DG⊥PC.
过G作GH⊥PC于H,则PC⊥面GHD,连接DH,则PC⊥DH,
∴∠GHD是二面角A﹣PC﹣D的平面角.
在△ADC中,![]() ,连接AE,
,连接AE,![]() .
.
在Rt△GDH中,![]() ,
,
∴![]() ,
,
即二面角A﹣PC﹣D的余弦值![]()
法二、取BC的中点M,连接AM,则AD∥MC,且AD=MC.
∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上,
∴AB⊥AC.
∵面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,∴AB⊥面PAC.
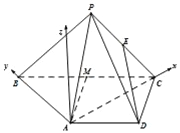
如图以A为原点,![]() 方向分别为x轴正方向,y轴正方向建立空间直角坐标系.
方向分别为x轴正方向,y轴正方向建立空间直角坐标系.
可得![]() ,
,![]() .
.
设P(x,0,z),(z>0),依题意有![]() ,
,![]() ,
,
解得![]() .
.
则![]() ,
,![]() ,
,![]() .
.
设面PDC的一个法向量为![]() ,
,
由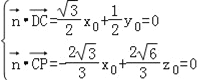 ,取x0=1,得
,取x0=1,得![]() .
.
![]()
![]() 为面PAC的一个法向量,且
为面PAC的一个法向量,且![]() ,
,
设二面角A﹣PC﹣D的大小为θ,
则有![]() ,即二面角A﹣PC﹣D的余弦值
,即二面角A﹣PC﹣D的余弦值![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4x+a2x+3,a∈R.
(1)当a=﹣4时,且x∈[0,2],求函数f(x)的值域;
(2)若关于x的方程f(x)=0在(0,+∞)上有两个不同实根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:椭圆 ![]() (a>b>0),过点
(a>b>0),过点 ![]() ,
, ![]() 的直线倾斜角为
的直线倾斜角为 ![]() ,原点到该直线的距离为
,原点到该直线的距离为 ![]() .
.
(1)求椭圆的方程;
(2)斜率大于零的直线过 ![]() 与椭圆交于E,F两点,若
与椭圆交于E,F两点,若 ![]() ,求直线EF的方程.
,求直线EF的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市出租车收费标准如下:①起步价3km(含3km)为10元;②超过3km以外的路程按2元/km收费;③不足1km按1km计费.
(1)试写出收费y元与x(km)(0<x≤5)之间的函数关系式;
(2)若某人乘出租车花了24元钱,求此人乘车里程xkm的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z的实部和虚部都是整数,
(1)若复数z为纯虚数,且|z﹣1|=|﹣1+i|,求复数z;
(2)若复数z满足z+ ![]() 是实数,且1<z+
是实数,且1<z+ ![]() ≤6,求复数z.
≤6,求复数z.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在近30天内每件的销售价格P(元)与时间t(天)的函数关系是P= ![]() ,该商场的日销售量Q=﹣t+40(0<t≤30,t∈N),求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天.
,该商场的日销售量Q=﹣t+40(0<t≤30,t∈N),求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com