
����Ŀ���±��е�������һ�ν��Կ���ij�����ѧ������ԭʼ�ɼ���

����44�˵����Ƴɼ���������ɢ��ͼ��

ѧ��Ϊ22�ŵ�![]() ͬѧ�������ظ�ð�����������Է���ʧ����ѧ��Ϊ31�ŵ�
ͬѧ�������ظ�ð�����������Է���ʧ����ѧ��Ϊ31�ŵ�![]() ͬѧ���δ�ܲμ�����ѧ�ƵĿ��ԣ�Ϊ��ʹ�����������ȷ����ʦ��
ͬѧ���δ�ܲμ�����ѧ�ƵĿ��ԣ�Ϊ��ʹ�����������ȷ����ʦ��![]() ��ͬѧ�ijɼ�����Ӧ��ͼ��
��ͬѧ�ijɼ�����Ӧ��ͼ��![]() ���㣩������ʣ�µ�42��ͬѧ������������������õ�����ͳ��ָ�꣺
���㣩������ʣ�µ�42��ͬѧ������������������õ�����ͳ��ָ�꣺
��ѧѧ��ƽ����Ϊ110.5������Ϊ18.36������ѧ�Ƶ�ƽ����Ϊ74������Ϊ11.18����ѧ�ɼ�![]()
�������ɼ�![]() �����ϵ��Ϊ
�����ϵ��Ϊ![]() ���ع�ֱ��
���ع�ֱ��![]() ����ͼ��ʾ���ķ���Ϊ
����ͼ��ʾ���ķ���Ϊ![]() .
.
��1��������![]() ��ͬѧ�����ݣ���ȫ��44�˵ijɼ����ع����������ѧ�ɼ�
��ͬѧ�����ݣ���ȫ��44�˵ijɼ����ع����������ѧ�ɼ�![]() �������ɼ�
�������ɼ�![]() �����ϵ��Ϊ
�����ϵ��Ϊ![]() ���ع�ֱ��Ϊ
���ع�ֱ��Ϊ![]() ���Է���
���Է���![]() ��
��![]() �Ĵ�С��ϵ������ͼ�л����ع�ֱ��
�Ĵ�С��ϵ������ͼ�л����ع�ֱ��![]() �Ĵ���λ�ã�
�Ĵ���λ�ã�
��2�����![]() ͬѧ�μ�������������ԣ�����
ͬѧ�μ�������������ԣ�����![]() ͬѧ��������������ȷ����λ����
ͬѧ��������������ȷ����λ����
��3������ο��Զ��ԣ�ѧ��Ϊ16�ŵ�![]() ͬѧ��ѧ�������ĸ�ѧ�Ƴɼ�Ҫ��һЩ����ͨ��Ϊ�˱Ƚ�ij��ѧ����ͬѧ�Ƶijɼ�ˮƽ���ɰ���ʽ
ͬѧ��ѧ�������ĸ�ѧ�Ƴɼ�Ҫ��һЩ����ͨ��Ϊ�˱Ƚ�ij��ѧ����ͬѧ�Ƶijɼ�ˮƽ���ɰ���ʽ![]() ͳһ���ɱ����ٽ��бȽϣ�����
ͳһ���ɱ����ٽ��бȽϣ�����![]() Ϊѧ��ԭʼ�֣�
Ϊѧ��ԭʼ�֣�![]() Ϊѧ��ƽ���֣�
Ϊѧ��ƽ���֣�![]() Ϊѧ�Ʊ����
Ϊѧ�Ʊ����
���𰸡���1��![]() �����ɼ�������2��81��3��
�����ɼ�������2��81��3��![]()
��������
��1������![]() ��ͬѧ�����ݣ�44�����ݻ�ʹ�ع�Ч�����Ӷ��õ�
��ͬѧ�����ݣ�44�����ݻ�ʹ�ع�Ч�����Ӷ��õ�![]() ������ع�ֱ���ɣ���2����x=125����ع�ֱ�߷��̣����ɵõ��𰸣���3��������Ŀ�����ı��ּ��㹫ʽ���м��㼴�ɵõ�����.
������ع�ֱ���ɣ���2����x=125����ع�ֱ�߷��̣����ɵõ��𰸣���3��������Ŀ�����ı��ּ��㹫ʽ���м��㼴�ɵõ�����.
(1)![]() ��
��
˵�����ɿ����ǣ�
����Ⱥ��A,B�ή�ͱ���������Թ����̶ȣ�
��44�����ݵ���ع�ֱ��![]() ����ƫ����ع�Ч������������ϵ����С��
����ƫ����ع�Ч������������ϵ����С��
��42�����ݵ���ع�ֱ��![]() ����ƫ���С���ع�Ч�����ã��������ϵ������
����ƫ���С���ع�Ч�����ã��������ϵ������
��42�����ݵ���������ع�ֱ��![]() ��
��
��44�����ݵ���ع�ֱ��![]() ����ɢ����������֮���������ɾ���.
����ɢ����������֮���������ɾ���.

Ҫ�㣺ֱ��![]() б�������0��С��
б�������0��С��![]() ��б�ʣ�����Ϊֹ���г���û��ϵ������˵������.
��б�ʣ�����Ϊֹ���г���û��ϵ������˵������.
��2����![]() ������
������![]()
��![]()
���ԣ�����![]() ͬѧ������������ԼΪ
ͬѧ������������ԼΪ![]() ��.
��.
��3���ɱ���֪![]() ͬѧ����ѧԭʼ��Ϊ122������ԭʼ��Ϊ82��
ͬѧ����ѧԭʼ��Ϊ122������ԭʼ��Ϊ82��
��ѧ����Ϊ![]()
��������Ϊ![]()
![]() ����
����![]() ͬѧ�����ɼ�����ѧ�ɼ�Ҫ��һЩ.
ͬѧ�����ɼ�����ѧ�ɼ�Ҫ��һЩ.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ִ������ij����ͼ�����![]() ��ֵΪ3�����жϿ���Ӧ����������ǣ� ��
��ֵΪ3�����жϿ���Ӧ����������ǣ� ��
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij���鼮ÿ��ijɱ���![]() ��Ԫ����ӡˢ����
��Ԫ����ӡˢ����![]() ��ǧ�ᣩ���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ.
��ǧ�ᣩ���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |

����![]() ��
��![]() .
.
Ϊ��Ԥ��ӡˢ![]() ǧ��ʱÿ��ijɱ����������������ع�ģ����
ǧ��ʱÿ��ijɱ����������������ع�ģ����![]() ��
��![]() .
.
��1������ɢ��ͼ������Ϊѡ���ĸ�ģ��Ԥ����ɿ�����ֻѡ��ģ�ͼ��ɣ�
��2�������������ݺͣ�1���е�ģ��ѡ����![]() ����
����![]() �Ļع鷽������Ԥ��ӡˢ
�Ļع鷽������Ԥ��ӡˢ![]() ǧ��ʱÿ��ijɱ���.
ǧ��ʱÿ��ijɱ���.
��������һ������![]() ��
��![]() ������
������![]() ����ع鷽��
����ع鷽��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ�� ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ���㣺
���㣺![]() Ϊ���������Ҷ�����������
Ϊ���������Ҷ�����������![]() ��
��![]() Ϊǰ
Ϊǰ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���
�е���![]() ����ĸ���.
����ĸ���.
��1����![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
��2����֪����![]() ����������
����������![]() ��ʹ��
��ʹ��![]() ���ж�����
���ж�����![]() ����ٲ�˵�����ɣ�
����ٲ�˵�����ɣ�
��3����������������![]() ������
������![]() ���������
���������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
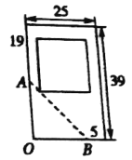
����Ŀ�������æ���2010��������������Сѧ����У�ᣬ��ͼ����ѧУ�Ķ�������һ��أ����������Dz��ܶ���Χǽ���ڱ߽�![]() ���Dz��ܶ���һЩ������ʩ�������ڴ˽�һ����ѧ¥��ʹ¥�ĵ���Ϊһ���Σ��ҿ�Χǽ�ķ���������5���Ŀյأ��������ƣ�����ʹ��ѧ¥��������
���Dz��ܶ���һЩ������ʩ�������ڴ˽�һ����ѧ¥��ʹ¥�ĵ���Ϊһ���Σ��ҿ�Χǽ�ķ���������5���Ŀյأ��������ƣ�����ʹ��ѧ¥��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����[x]Ϊ������ʵ��x��������������磬[2]=2��[1.5]=1��[��0.3]=��1����aΪ������������{xn}����x1=a�� ![]() �������������⣺
�������������⣺
�ٵ�a=5ʱ������{xn}��ǰ3������Ϊ5��3��2��
�ڶ�����{xn}������������k����n��kʱ����xn=xk��
�۵�n��1ʱ�� ![]() ��
��
�ܶ�ij��������k����xk+1��xk �� �� ![]() ��
��
���е��������� �� ��д������������ı�ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������װ��![]() ����С��ͬ�ĺ���Ͱ���.��֪�Ӵ�����������
����С��ͬ�ĺ���Ͱ���.��֪�Ӵ�����������![]() �������ٵõ�
�������ٵõ�![]() ������ĸ�����
������ĸ�����![]() .
.
��1�������ĸ�����
��2���Ӵ�����������![]() ���ǵõ�����ĸ���Ϊ
���ǵõ�����ĸ���Ϊ![]() �����������
�����������![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪aΪ��ʵ����nΪ��Ȼ���������� ![]() ��x���������ཻ�ڵ�A����f��n��Ϊ���������ڵ�A����������y���ϵĽؾ࣮
��x���������ཻ�ڵ�A����f��n��Ϊ���������ڵ�A����������y���ϵĽؾ࣮
��1����a��n��ʾf��n����
��2���������n���� ![]() ������a����Сֵ��
������a����Сֵ��
��3����0��a��1ʱ���Ƚ� ![]() ��
�� ![]() �Ĵ�С����˵�����ɣ�
�Ĵ�С����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���߶�
���߶�![]() ���е㡣
���е㡣

��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2�������߶�![]() ��ȷ��һ��
��ȷ��һ��![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ��������֤����
��������֤����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com