练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．若函数y=$\frac{kx+2016}{k{x}^{2}+4kx+3}$的定义域为R，则实数k的取值范围是[0，$\frac{3}{4}$）．

    分析 由函数y=$\frac{kx+2016}{k{x}^{2}+4kx+3}$的定义域为R，可得对任意实数x，kx2+4kx+3恒不等于0，然后分k=0和k≠0讨论，当k≠0时，由△＜0得答案．

    解答 解：∵函数y=$\frac{kx+2016}{k{x}^{2}+4kx+3}$的定义域为R，
    ∴对任意实数x，kx2+4kx+3恒不等于0，
    当k=0时，kx2+4kx+3=3≠0满足题意；
    当k≠0时，需△=16k2-12k＜0，即0$＜k＜\frac{3}{4}$．
    综上，实数k的取值范围是[0，$\frac{3}{4}$）．
    故答案为：[0，$\frac{3}{4}$）．

    点评 本题考查函数恒成立问题，考查了分类讨论的数学思想方法，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．将下列三角函数转化为锐角三角函数，并填在题中横线上：
    （1）cos210°=-cos30°；
    （2）sin263°42′=-sin83°42′；
    （3）cos（-$\frac{π}{6}$）cos$\frac{π}{6}$； 
    （4）sin（-$\frac{5}{3}$π）=sin$\frac{π}{3}$；
    （5）cos（-$\frac{11}{9}$π）=-cos$\frac{π}{9}$；
    （6）cos（-104°26′）=-sin14°26′；
    （7）tan632°24′=-tan87°36′；
    （8）tan$\frac{17π}{6}$=-tan$\frac{π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．有下列关系：（1）人的年龄与他（她）体内脂肪含量之间的关系；（2）曲线上的点与该点的坐标之间的关系；（3）红橙的产量与气候之间的关系；（4）学生与他（她）的学号之间的关系．其中有相关关系的是（　　）
    A．（1）、（2）B．（1）、（3）C．（1）、（4）D．（3）、（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知空间四点A（1，0，0），B（0，1，0），C（0，0，1），P（2，3，m）同在平面α内，则m的值为-4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知集合M={x|1＜x＜4}，集合N={x|3＜x＜6}．
    （1）求M∩N，∁RN；
    （2）设A={x|a＜x＜a+4}，若A∪∁RN=R，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知集合A={0，2，3}，B={x|x=ab，a，b∈A且a≠b}，则B的子集有4个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设0＜α＜π，0＜β＜π，$\overrightarrow{a}$=（cosα，sinα），$\overrightarrow{b}$=（1-cosβ，sinβ），且$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{2}$-cosβ
    （Ⅰ）求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ
    （Ⅱ）求α、β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

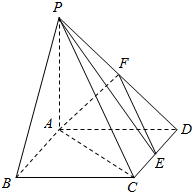    6．如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，且PA=AD，点F是棱PD的中点，点E在棱CD上移动．求证：PE⊥AF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．在△ABC中，a，b，c分别为内角A，B，C的对边，三边a，b，c成等差数列，且$B=\frac{π}{4}$，则（cosA-cosC）2的值为$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案