
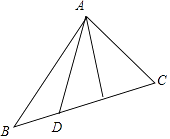
【题目】△ABC中,sin(A﹣B)=sinC﹣sinB,D是边BC的一个三等分点(靠近点B),记 ![]() ,则当λ取最大值时,tan∠ACD= .
,则当λ取最大值时,tan∠ACD= .
【答案】2+ ![]()
【解析】解:∵sin(A﹣B)=sinC﹣sinB, ∴sinAcosB﹣cosAsinB=sinC﹣sinB=sinAcosB+cosAsinB﹣sinB,
∴sinB=2cosAsinB,∵sinB≠0,
∴cosA= ![]() ,由A∈(0,π),可得:A=
,由A∈(0,π),可得:A= ![]() ,
,
在△ADB中,由正弦定理可将 ![]() ,变形为则
,变形为则 ![]() ,
,
∵ ![]() =
= ![]()
∴ ![]() 即a2λ2=4c2+b2+2bc…①
即a2λ2=4c2+b2+2bc…①
在△ACB中,由余弦定理得:a2=b2+c2﹣bc…②
由①②得 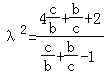
令 ![]() ,
, 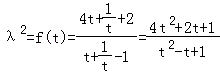 ,f′(t)=
,f′(t)= ![]() ,令f′(t)=0,得t=
,令f′(t)=0,得t= ![]() ,
,
即 ![]() 时,λ最大.
时,λ最大.
结合②可得b= ![]() ,a=
,a= ![]() c
c
在△ACB中,由正弦定理得 ![]()
![]() ,tanC=2+
,tanC=2+ ![]()
所以答案是:2+ ![]() .
.
【考点精析】通过灵活运用正弦定理的定义,掌握正弦定理:![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是 ![]() 或
或 ![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() ,
, ![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是 ![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,F1、F2分别是椭圆的左、右焦点,M为椭圆上除长轴端点外的任意一点,且△MF1F2的周长为4+2
,F1、F2分别是椭圆的左、右焦点,M为椭圆上除长轴端点外的任意一点,且△MF1F2的周长为4+2 ![]() .
.
(1)求椭圆C的方程;
(2)过点D(0,﹣2)作直线l与椭圆C交于A、B两点,点N满足 ![]() (O为原点),求四边形OANB面积的最大值,并求此时直线l的方程.
(O为原点),求四边形OANB面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f (x0)=3,x0∈( ![]() ,
, ![]() ),则sinx0的值为( )
),则sinx0的值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
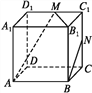
【题目】如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:
①直线AM与CC1是相交直线;②直线AM与BN是平行直线;
③直线BN与MB1是异面直线; ④直线MN与AC所成的角为60°.
其中正确的结论为___ (注:把你认为正确的结论序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角, ![]() , 平面ABCD⊥平面ABFE.
, 平面ABCD⊥平面ABFE.
(1)求证:DB⊥EC;
(2)若AE=AB,求二面角C﹣EF﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (
( ![]() 为实常数).
为实常数).
(1)若 ![]() ,
, ![]() ,求
,求 ![]() 的单调区间;
的单调区间;
(2)若 ![]() ,且
,且 ![]() ,求函数
,求函数 ![]() 在
在 ![]() 上的最小值及相应的
上的最小值及相应的 ![]() 值;
值;
(3)设 ![]() ,若存在
,若存在 ![]() ,使得
,使得 ![]() 成立,求实数
成立,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com