Question

【题目】已知椭圆过点，右焦点是抛物线的焦点.

（1）求椭圆的方程；

（2）已知动直线过右焦点，且与椭圆分别交于，两点.试问轴上是否存在定点，使得恒成立?若存在求出点的坐标:若不存在，说明理由.

Answer 1

【答案】(1) (2)见解析

【解析】

(1) 由椭圆过点，得，由抛物线的焦点为，得，利用即可求解a则方程可求；（2）假设在轴上存在定点，当直线的斜率不存在时，由，解得或；当直线的斜率为0时，由，解得或，可得，得点的坐标为.再证明当时恒成立. 设直线的斜率存在且不为0时，其方程为，与椭圆联立消去y得韦达定理,向量坐标化得整理代入韦达定理即可

（1）因为椭圆过点，所以，

又抛物线的焦点为，所以.

所以，解得（舍去）或.

所以椭圆的方程为.

（2）假设在轴上存在定点，使得.

①当直线的斜率不存在时，则，，，，

由，解得或；

②当直线的斜率为0时，则，，，，

由，解得或.

由①②可得，即点的坐标为.

下面证明当时，恒成立.

当直线的斜率不存在或斜率为0时，由①②知结论成立.

当直线的斜率存在且不为0时，设其方程为，，.直线与椭圆联立得，

直线经过椭圆内一点，一定与椭圆有两个交点，且，.

，

所以

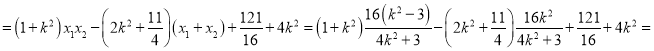
恒成立

综上所述，在轴上存在点，使得恒成立.