
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,
,![]() .
.
(1)求以线段![]() 为邻边的平行四边形的另一顶点
为邻边的平行四边形的另一顶点![]() 的坐标;
的坐标;
(2)求证:![]() .
.
【答案】(1)(1,4) (2)详见解析
【解析】
(1)利用向量坐标表示![]() ,从而得解;
,从而得解;
(2)利用向量坐标表示,证明向量的数量积为0即可.
(1) 解:法1:∵![]() =(3,5),设D(x,y),则
=(3,5),设D(x,y),则![]() =(x+2,y+1),
=(x+2,y+1),
∵![]() =
=![]() ,∴
,∴![]() 即D(1,4);
即D(1,4);
法2:因为B、C的中点坐标为(0,1),设D(x,y)
则A、D的中点坐标为![]()
因为平行四边形的对角线互相平分,所以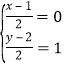 ,
,
解得![]()
即D(1,4)
(2)证明: 法1:![]() =(-2,-1),∵(
=(-2,-1),∵(![]() +
+![]()
![]() )·
)·![]() =
=![]() ·
·![]() +
+![]()
![]() 2,
2,
而![]() ·
·![]() =3×(-2)+5×(-1)=-11,
=3×(-2)+5×(-1)=-11,![]() 2=5
2=5
代入上式得(![]() +
+![]()
![]() )·
)·![]() =0
=0
所以(![]() +
+![]()
![]() )⊥
)⊥![]()
法2:因为![]() =(3,5),
=(3,5),![]() =(-2,-1),
=(-2,-1),
所以![]() +
+![]()
![]() =
=![]()
所以(![]() +
+![]()
![]() )·
)·![]() =
=![]() ·(-2,-1)=0
·(-2,-1)=0
所以(![]() +
+![]()
![]() )⊥
)⊥![]()


科目:高中数学 来源: 题型:
【题目】在公比为2的等比数列{an}中,a2与a3的等差中项是9 ![]() .
.
(1)求a1的值;
(2)若函数y=|a1|sin( ![]() x+φ),|φ|<π,的一部分图象如图所示,M(﹣1,|a1|),N(3,﹣|a1|)为图象上的两点,设∠MPN=β,其中P与坐标原点O重合,0<β<π,求tan(φ﹣β)的值.
x+φ),|φ|<π,的一部分图象如图所示,M(﹣1,|a1|),N(3,﹣|a1|)为图象上的两点,设∠MPN=β,其中P与坐标原点O重合,0<β<π,求tan(φ﹣β)的值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣x2﹣ax.
(1)若曲线y=f(x)在点x=0处的切线斜率为1,求函数f(x)在[0,1]上的最值;
(2)令g(x)=f(x)+ ![]() (x2﹣a2),若x≥0时,g(x)≥0恒成立,求实数a的取值范围;
(x2﹣a2),若x≥0时,g(x)≥0恒成立,求实数a的取值范围;
(3)当a=0且x>0时,证明f(x)﹣ex≥xlnx﹣x2﹣x+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求实数![]() 的值;
的值;
(2)当![]() 时,函数
时,函数![]() 存在零点,求实数
存在零点,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若函数
,若函数![]() 与
与![]() 的图像只有一个公共点,求实数
的图像只有一个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校的学生文娱团队由理科组和文科组构成,具体数据如表所示:
组别 | 文科 | 理科 | ||
性别 | 男生 | 女生 | 男生 | 女生 |
人数 | 3 | 1 | 3 | 2 |
学校准备从该文娱团队中选出4人到某社区参加大型公益活动演出,每选出一名男生,给其所在的组记1分;每选出一名女生,给其所在的组记2分,要求被选出的4人中文科组和理科组的学生都有.
(I)求理科组恰好得4分的概率;
(II)记文科组的得分为X,求随机变量X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 都是边长为
都是边长为![]() 的等边三角形,
的等边三角形,![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一动点,记
上一动点,记![]() .
.
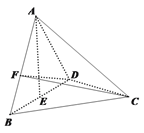
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式x2+y2≤4确定的平面区域为U,|x|+|y|≤1确定的平面区域为V.
(1)定义横、纵坐标为整数的点为“整点”,在区域U内任取3个整点,求这些整点中恰有2个整点在区域V的概率;
(2)在区域U内任取3个点,记这3个点在区域V的个数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com