【题目】在水平地面上的不同两点处栽有两根笔直的电线杆，假设它们都垂直于地面，则在水平地面上视它们上端仰角相等的点
的轨迹可能是（ ）
①直线 ②圆 ③椭圆 ④抛物线
A.①②B.①③C.①②③D.②④
【答案】A
【解析】
讨论两根电线杆是否相等.当两个电线杆的高度相等时,到上端仰角相等的点在地面上为两根电线底部连线的垂直平分线.当两个电线杆的高度不同时,在底面建立平面直角坐标系,可根据轨迹方程的求法求解.
当两根电线杆的高度相等时,因为在水平地面上视它们上端仰角相等
所以由垂直平分线的定义可知,点
的轨迹为两根电线底部连线的垂直平分线,即轨迹为一条直线
当两根电线的高度不同时,如下图所示:
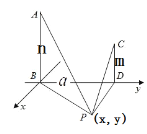
在地面上以B为原点,以BD所在直线为
轴
设
,
,
由题意可知,
,即
所以满足
,即
由两点间距离公式,代入可得
化简可得
,
即
二次项的系数相同,且满足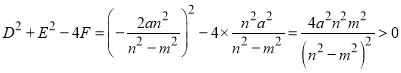
所以此时动点的轨迹为圆
综上可知,点的轨迹可能是直线,也可能是圆
故选:A
科目：高中数学 来源： 题型：
【题目】用计算机生成随机数表模拟预测未来三天降雨情况，规定1，2，3表示降雨，4，5，6，7，8，9表示不降雨，根据随机生成的10组三位数：654 439 565 918 288 674 374 968 224 337，则预计未来三天仅有一天降雨的概率为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
上一点
到焦点
的距离
.
（1）求抛物线
的方程；
（2）过点
引圆
的两条切线
，切线与抛物线的另一交点分别为
，线段
中点的横坐标记为
，求的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
，
是
的导函数.
（1）若
，求
的值；
（2）设
.①若函数
在定义域上单调递增，求的取值范围；②若函数在定义域上不单调，试判定的零点个数，并给出证明过程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，以原点为极点，x轴正半轴为极轴建立极坐标系，并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为
，直线l的参数方程为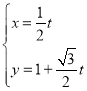
，（t为参数）.
（1）求直线l的普通方程和曲线C的直角坐标方程；
（2）若直线l与曲线C交于A，B两点，
，且
，求
值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某快递网点收取快递费用的标准是重量不超过
的包裹收费10元，重量超过的包裹，除收费10元之外，超过的部分，每超出（不足，按计算）需要再收费5元．该公司近60天每天揽件数量的频率分布直方图如下图所示（同一组数据用该区间的中点值作代表）．
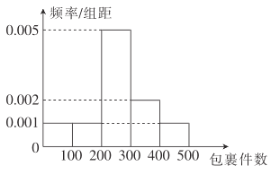
（1）求这60天每天包裹数量的平均数和中位数；
（2）该快递网点负责人从收取的每件快递的费用中抽取5元作为工作人员的工资和网点的利润，剩余的作为其他费用．已知该网点有工作人员3人，每人每天工资100元，以样本估计总体，试估计该网点每天的利润有多少元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某调查机构对全国互联网行业进行调查统计，得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图，则下列结论中一定正确的是（ ）
（注：90后指1990年及以后出生，80后指1980-1989年之间出生，80前指1979年及以前出生）．
A.互联网行业从业人员中80前占3%以上
B.互联网行业90后中，从事设计岗位的人数比从事市场岗位的人数要多
C.互联网行业中从事技术岗位的人数超过总人数的20%
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
