
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 存在极大值
存在极大值![]() ,证明:
,证明:![]() ;
;
(2)若关于![]() 的不等式
的不等式![]() 在区间
在区间![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)![]() .(x∈(0,+∞)).对a分类讨论,即可得出单调性极值.进而证明结论.
.(x∈(0,+∞)).对a分类讨论,即可得出单调性极值.进而证明结论.
(2)令h(x)=f(x)+ex-1-1=lnx-ax+a+ex-1-1,x∈[1,+∞),h(1)=0.![]() ,
,![]() ,对a分类讨论,利用导数研究函数的单调性、极值与最值即可得出.
,对a分类讨论,利用导数研究函数的单调性、极值与最值即可得出.
(1)![]()
当![]() 时,
时,![]() ,
,![]() 单调递增,不存在极大值,
单调递增,不存在极大值,
所以![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]() 的极大值为
的极大值为![]() .
.
设![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,![]() .
.
所以![]() 的极大值大于等于0.
的极大值大于等于0.
(2)设![]() ,
,
![]() ,
,![]() ,
,
所以![]() 单调递增,
单调递增,
由![]() 知
知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() 在
在![]() 恒成立,
恒成立,
此时,函数![]() 在
在![]() 上单调递增,
上单调递增,![]() ,满足条件.
,满足条件.
若![]() ,则
,则![]() ,所以存在
,所以存在![]() 使得
使得![]() ,
,
即在![]() 内,有
内,有![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() 不满足条件.
不满足条件.
综上,![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】现代足球运动是世上开展得最广泛、影响最大的运动项目,有人称它为“世界第一运动”.早在2000多年前的春秋战国时代,就有了一种球类游戏“蹴鞠”,后来经过阿拉伯人传到欧洲,发展成现代足球.1863年10月26日,英国人在伦敦成立了世界上第一个足球运动组织——英国足球协会,并统一了足球规则.人们称这一天是现代足球的诞生日.如图所示,足球表面是由若干黑色正五边形和白色正六边形皮围成的,我们把这些正五边形和正六边形都称为足球的面,任何相邻两个面的公共边叫做足球的棱.已知足球表面中的正六边形的面为20个,则该足球表面中的正五边形的面为______个,该足球表面的棱为______条.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知倾斜角为
中,已知倾斜角为![]() 的直线
的直线![]() 过点
过点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.曲线
轴的正半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() ,求直线
,求直线![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() =1(a>0,b>0)的左右焦点为F1,F2过点F1的直线l与双曲线C的左支交于AB两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为( )
=1(a>0,b>0)的左右焦点为F1,F2过点F1的直线l与双曲线C的左支交于AB两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
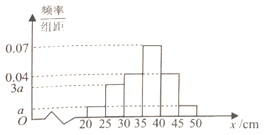
【题目】某农科站技术员为了解某品种树苗的生长情况,在该批树苗中随机抽取一个容量为100的样本,测量树苗高度(单位:![]() ).经统计,高度在区间
).经统计,高度在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图,其中高度不低于
分成6组,制成如图所示的频率分布直方图,其中高度不低于![]() 的树苗为优质树苗.
的树苗为优质树苗.
附:
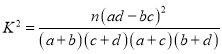 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
(1)求频率分布直方图中![]() 的值;
的值;
(2)已知所抽取的这100棵树苗来自于甲、乙两个地区,部分数据如下![]() 列联表所示,将列联表补充完整,并根据列联表判断是否有
列联表所示,将列联表补充完整,并根据列联表判断是否有![]() %的把握认为优质树苗与地区有关?
%的把握认为优质树苗与地区有关?
甲地区 | 乙地区 | 合计 | |
优质树苗 | 5 | ||
非优质树苗 | 25 | ||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某工厂每天固定成本是4万元,每生产一件产品成本增加100元,工厂每件产品的出厂价定为![]() 元时,生产
元时,生产![]() 件产品的销售收入是
件产品的销售收入是![]() (元),
(元),![]() 为每天生产
为每天生产![]() 件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件
件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件![]() 元进货后又以每件
元进货后又以每件![]() 元销售,
元销售, ![]() ,其中
,其中![]() 为最高限价
为最高限价![]() ,
, ![]() 为销售乐观系数,据市场调查,
为销售乐观系数,据市场调查, ![]() 是由当
是由当![]() 是
是![]() ,
, ![]() 的比例中项时来确定.
的比例中项时来确定.
(1)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 取得最大值?并求
取得最大值?并求![]() 的最大值;
的最大值;
(2)求乐观系数![]() 的值;
的值;
(3)若![]() ,当厂家平均利润最大时,求
,当厂家平均利润最大时,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为
(a>b>0)的左焦点为F,上顶点为B. 已知椭圆的离心率为![]() ,点A的坐标为
,点A的坐标为![]() ,且
,且![]() .
.
(I)求椭圆的方程;
(II)设直线l: ![]() 与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若
与椭圆在第一象限的交点为P,且l与直线AB交于点Q. 若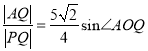 (O为原点) ,求k的值.
(O为原点) ,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com