
【题目】一个盒子内装有8张卡片,每张卡片上面写着1个数字,这8个数字各不相同,且奇数有3个,偶数有5个.每张卡片被取出的概率相等.
(Ⅰ)如果从盒子中一次随机取出2张卡片,并且将取出的2张卡片上的数字相加得到一个新数,求所得新数是偶数的概率;
(Ⅱ)现从盒子中一次随机取出1张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的数是偶数则停止取出卡片,否则继续取出卡片.设取出了![]() 次才停止取出卡片,求
次才停止取出卡片,求![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到数据如表所示(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | 8 | |
不肥胖 | 18 | ||
合计 | 30 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
| 0.050 0.010 |
| 3.841 6.635 |
参考数据:
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 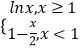 ,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
A.[4﹣2ln2,+∞)
B.( ![]() ,+∞)
,+∞)
C.(﹣∞,4﹣2ln2]
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() =1(a>0,b>0),过其左焦点F作x轴的垂线,交双曲线于A,B两点,若双曲线的右顶点在以AB为直径的圆外,则双曲线离心率的取值范围是( )
=1(a>0,b>0),过其左焦点F作x轴的垂线,交双曲线于A,B两点,若双曲线的右顶点在以AB为直径的圆外,则双曲线离心率的取值范围是( )
A.(1, ![]() )
)
B.(1,2)
C.( ![]() ,+∞)
,+∞)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E= ![]() .
.
(Ⅰ)证明:A1D⊥平面A1BC;
(Ⅱ)求二面角A﹣BD﹣B1的平面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com