
分析 对a分类分析,可知当a>0时,函数f(x)=x+$\frac{a}{x}$+1的值域符合题意,求出其值域,结合f(x)=x+$\frac{a}{x}$+1的值域为(-∞,-1]∪[3,+∞)列关于a的方程组求a
解答 解:若a=0,f(x)=x+$\frac{a}{x}$+1=x+1,值域为(-∞,+∞),不满足题意;
若a<0,f(x)=x+$\frac{a}{x}$+1在(-∞,0),(0,+∞)上为增函数,函数f(x)=x+$\frac{a}{x}$+1的值域为(-∞,+∞),不满足题意;
若a>0,则当x>0时,f(x)=x+$\frac{a}{x}$+1≥2$\sqrt{x•\frac{a}{x}}$+1=2$\sqrt{a}$+1,当且仅当x=$\sqrt{a}$时取“=”;
当x<0时,f(x)=x+$\frac{a}{x}$+1≤-2$\sqrt{-x•\frac{a}{-x}}$+1=-2$\sqrt{a}$+1,当且仅当x=-$\sqrt{a}$时取“=”.
由$\left\{\begin{array}{l}2\sqrt{a}+1=3\\-2\sqrt{a}+1=-1\end{array}\right.$,
解得a=1,
故答案为:1.
点评 本题考查函数值域的求法,训练了利用基本不等式求最值,体现了分类讨论的数学思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1 | B. | $\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1 | C. | $\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1 | D. | $\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
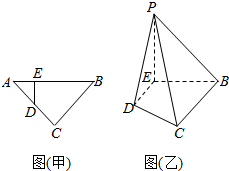 如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙))
如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙))查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com