
【题目】2020年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | 30 | ||
女生 | 15 | ||
合计 | 120 |
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
【答案】(1)表格见解析,有99%的把握认为对“线上教育是否满意与性别有关”;(2)分布列见解析,![]()
【解析】
(1)根据男生与女生的人数之比为11∶13,以及总人数120,可求出男,女生总人数,即可完成![]() 列联表,并根据独立性检验的基本思想,求出
列联表,并根据独立性检验的基本思想,求出![]() 的观测值,对照临界值表,即可判断是否有把握;
的观测值,对照临界值表,即可判断是否有把握;
(2)根据(1)可知,男生抽3人,女生抽5人,于是,离散型随机变量 的可能取值为![]() ,并且服从超几何分布,即可利用公式
,并且服从超几何分布,即可利用公式![]() (
(![]() ),求出各概率,得到分布列,求出期望
),求出各概率,得到分布列,求出期望
(1)因为男生人数为:![]() ,所以女生人数为
,所以女生人数为![]() ,
,
于是可完成![]() 列联表,如下:
列联表,如下:
满意 | 不满意 | 总计 | |
男生 | 30 | 25 | 55 |
女生 | 50 | 15 | 65 |
合计 | 80 | 40 | 120 |
根据列联表中的数据,得到![]() 的观测值
的观测值
![]() ,
,
所以有99%的把握认为对“线上教育是否满意与性别有关”.
(2)由(1)可知男生抽3人,女生抽5人,
依题可知![]() 的可能取值为
的可能取值为![]() ,并且
,并且![]() 服从超几何分布,
服从超几何分布,![]() (
(![]() ),即
),即
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
可得分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
可得![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AD.M,N分别是AB,PC的中点.
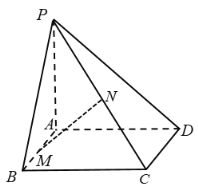
(1)求证:MN//平面PAD;
(2)求证:MN⊥平面PCD;
(3)求二面角B—PC—D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下几个命题中:
①线性回归直线方程![]() 恒过样本中心
恒过样本中心![]() ;
;
②用相关指数![]() 可以刻画回归的效果,值越小说明模型的拟合效果越好;
可以刻画回归的效果,值越小说明模型的拟合效果越好;
③随机误差是引起预报值![]() 和真实值
和真实值![]() 之间存在误差的原因之一,其大小取决于随机误差的方差;
之间存在误差的原因之一,其大小取决于随机误差的方差;
④在含有一个解释变量的线性模型中,相关指数![]() 等于相关系数
等于相关系数![]() 的平方.
的平方.
其中真命题为 _________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
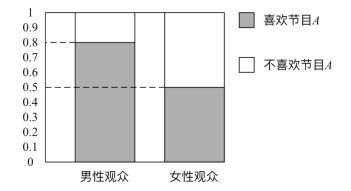
根据该等高条形图,完成下列2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 | 60 |
附: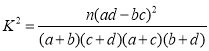
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,正三角形PAC所在平面与等腰三角形ABC所在平面互相垂直,AB=BC,O是AC中点,OH⊥PC于H.
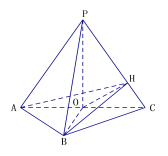
(1)证明:PC⊥平面BOH;
(2)若![]() ,求二面角A-BH-O的余弦值.
,求二面角A-BH-O的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.则下列结论中表述不正确的是( )
(单位:亿元)的折线图.则下列结论中表述不正确的是( )
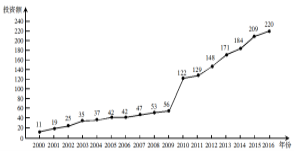
A. 从2000年至2016年,该地区环境基础设施投资额逐年增加;
B. 2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;
C. 2012年该地区基础设施的投资额比2004年的投资额翻了两番 ;
D. 为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为![]() )建立了投资额y与时间变量t的线性回归模型
)建立了投资额y与时间变量t的线性回归模型![]() ,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com