
 如图在扇形AOB中,OA=OB=1,∠AOB=1弧度,圆C是扇形AOB的内切圆,圆C与OA切于T点.
如图在扇形AOB中,OA=OB=1,∠AOB=1弧度,圆C是扇形AOB的内切圆,圆C与OA切于T点.分析 (1)直接通过求解直角三角形得圆C的半径r;
(2)求解直角三角形可得|$\overrightarrow{OT}$|=tan($\frac{π}{4}$-$\frac{1}{4}$);
(3)把($\overrightarrow{OP}$•$\overrightarrow{AP}$)•tan<$\overrightarrow{OP}$,$\overrightarrow{AP}$>转化为三角形OAP的面积分析,可知当三角形OAP面积最大时,($\overrightarrow{OP}$•$\overrightarrow{AP}$)•tan<$\overrightarrow{OP}$,$\overrightarrow{AP}$>最大.由此比较出|$\overrightarrow{AP}$|与|$\overrightarrow{OT}$|的大小.
解答 (1)解:在Rt△OTC中,sin$\frac{1}{2}$=$\frac{r}{1-r}$,则r=$\frac{sin\frac{1}{2}}{1+sin\frac{1}{2}}$;
(2)证明:由图可知,tan$\frac{1}{2}$=$\frac{r}{|\overrightarrow{OT}|}$,
∴|$\overrightarrow{OT}$|=$\frac{r}{tan\frac{1}{2}}=\frac{\frac{sin\frac{1}{2}}{1+sin\frac{1}{2}}}{tan\frac{1}{2}}$=$\frac{cos\frac{1}{2}}{1+sin\frac{1}{2}}$,
∵tan($\frac{π}{4}$-$\frac{1}{4}$)=tan$\frac{\frac{π}{2}-\frac{1}{2}}{2}$=$\frac{sin(\frac{π}{2}-\frac{1}{2})}{1+cos(\frac{π}{2}-\frac{1}{2})}$=$\frac{cos\frac{1}{2}}{1+sin\frac{1}{2}}$,
∴|$\overrightarrow{OT}$|=tan($\frac{π}{4}$-$\frac{1}{4}$);
(3)解:由($\overrightarrow{OP}$•$\overrightarrow{AP}$)•tan<$\overrightarrow{OP}$,$\overrightarrow{AP}$>=$|\overrightarrow{OP}|•|\overrightarrow{AP}|•cos$<$\overrightarrow{OP}$,$\overrightarrow{AP}$>•tan<$\overrightarrow{OP}$,$\overrightarrow{AP}$>
=$|\overrightarrow{OP}|•|\overrightarrow{AP}|sin$<$\overrightarrow{OP}$,$\overrightarrow{AP}$>=$\frac{1}{2}$S△OAP,
∴当P为TC的延长线与圆的交点时,($\overrightarrow{OP}$•$\overrightarrow{AP}$)•tan<$\overrightarrow{OP}$,$\overrightarrow{AP}$>最大.
∵$\frac{cos\frac{1}{2}}{1+sin\frac{1}{2}}$$>\frac{1}{2}$,
∴|$\overrightarrow{AP}$|<|$\overrightarrow{OT}$|.
点评 本题考查平面向量的数量积运算,考查了直角三角形的求解方法,考查数学中思想方法,属中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
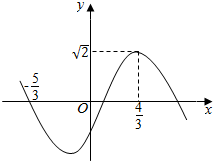 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(x)=x+1 | B. | f(x)=lnex与g(x)=elnx | ||
| C. | f(x)=|x|与g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=$\sqrt{x-1}$•$\sqrt{x+1}$与g(x)=$\sqrt{{x}^{2}-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(a)}{a}$>$\frac{f(b)}{b}$>$\frac{f(c)}{c}$ | B. | $\frac{f(c)}{c}$>$\frac{f(b)}{b}$>$\frac{f(a)}{a}$ | C. | $\frac{f(b)}{b}$>$\frac{f(a)}{a}$>$\frac{f(c)}{c}$ | D. | $\frac{f(a)}{a}$>$\frac{f(c)}{c}$>$\frac{f(b)}{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com